carte mental de maths 6éme Géometrie
6. Parallélépipèdes rectangles. Volumes
Le parallélépipède rectangle

Définition : un parallélépipède rectangle est un solide dont toutes les faces sont des rectangles.
les sommets sont les points ,
les faces du parallélépipède rectangle sont des rectangles.
L’image ci-dessus (le solide bleu) te fournit un exemple.
Définition : un parallélépipède rectangle dont toutes les faces sont des carrés est appelé un cube.
les sommets sont les points .
les faces du cube sont des carrés.
L’image ci-dessus (le solide vert) te fournit un exemple.
Définition : une arête est un segment dont les extrémités sont deux sommets consécutifs.
Propriété : un parallélépipède rectangle a huit sommets, six faces et douze arêtes.
Patron d’un parallélépipède rectangle
Définition : un patron d’un parallélépipède rectangle est une figure, qui, si elle est découpée et pliée convenablement, permet de fabriquer le parallélépipède rectangle en réalité.
Volume d’un parallélépipède rectangle
Le volume d’un parallélépipède rectangle est le produit de ses trois dimensions.
Remarque : les dimensions doivent toutes être exprimées dans la même unité. Au besoin, on les convertit dans la même unité.
1.Droite, règle, équerre
les bases
Les points, droites, demi-droites, segments et cercles sont les figures de base de la géométrie. On a représenté ci-dessous une droite, un segment, une demi-droite et un cercle :

Droites
Définition : on dit que deux droites sont sécantes lorsqu’elles ont un point commun et un seul.
Définition : deux droites sécantes qui forment un angle droit sont appelées des droites perpendiculaires.
Définition : deux droites qui ne sont pas sécantes sont appelées des droites parallèles.
Propriété 1 : si deux droites sont perpendiculaires à une même troisième droite, alors elles sont parallèles.
Cela s’écrit également : si et alors
Propriété 2 : soit deux droites parallèles. Si une troisième droite est perpendiculaire à l’une de ces deux droites, alors elle est perpendiculaire à l’autre.
Cela s’écrit également : si et alors
Propriété 3 : si deux droites sont parallèles à une troisième droite, alors elles sont parallèles entre elles.
Cela s’écrit également : si et alors
Médiatrice
Définition : la médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
Remarque : cette définition signifie que la médiatrice d’un segment est la seule droite qui :
est perpendiculaire au segment ;
le coupe en son milieu.
2. LES ANGLES
Angles
Un angle se note généralement à l’aide de trois lettres : il correspond à l’écartement existant entre deux demi-droites de même origine.
L’angle ci-dessous se note AOB ou BOA. Le sommet de l’angle est O. Les côtés de l’angle sont les demi-droites [OA) et [OB).

Mesure d’un angle
On mesure un angle à l’aide d’un rapporteur. L’unité d’angle est le degré, noté °.
Il existe quatre types d’angle : les angles aigus, droits, obtus et plats
Angles égaux
Définition : lorsque deux angles ont même mesure, on dit qu’ils sont égaux voici l'exemple de deux angles égaux:

Angles adjacents
Définition : deux angles sont adjacents s’ils ont le même sommet, un côté en commun, et s’ils sont situés de part et d’autre de ce côté commun.

Bissectrice d’un angle

Définition : La bissectrice d’un angle est la demi-droite qui le partage en deux angles adjacents égaux
Triangles particuliers
Définition : un triangle est rectangle lorsqu’il a un angle droit.
Définition: un triangle est isocèle lorsqu’il a au moins deux côtés de même longueur.
Définition : un triangle est équilatéral lorsque ses trois côtés ont la même longueur.
5. Aires et périmètres
Aire et Périmètre
Périmètre : le périmètre d’une figure est la longueur de son contour.
Aire : les deux surfaces ci-dessous n’ont pas la même forme, mais elles occupent autant de place. On dit alors qu’elles ont la même aire.
Exemple : le périmètre (en cm) de la figure ci-dessous est :
1,8 + 3 + 2,6 + 1,8 + 2,4 + 3
soit 14,6 cm.

Périmètre et aire d’un rectangle
Le périmètre P d’un rectangle de longueur L et de largeur est : P = 2 x (L+l). Son aire A est telle que : A = L x l
Périmètre et aire d’un carré
Le périmètre P d’un carré de côté c est :P = 4 x c Son aire A est telle que :A = c x c c’est-à-dire :A= c²
Périmètre et aire d’un triangle rectangle
Le périmètre P du triangle rectangle est tel que:P= a + b + c Son aire A est telle que : A = a x b / 2 se signe / signifie diviser
Longueur d’un cercle
La longueur L d’un cercle de diamètre D (ou de rayon r) est donnée par la formule : L = π x D c’est-à-dire :L =2 x π x R
Aire d’un disque
L’aire A d’un disque de rayon R est donnée par la formule : A = π R²
4. Quadrilatères
Quadrilatère
Définition : un quadrilatère est une figure fermée à quatre côtés, quatre sommets, quatre angles.
Exemple :

A,B,C ou d est l’un de ses sommets, Â,B,C ou D est l’un de ses angles. pour précision B , C et D sont pareil que Â
Définition : les diagonales d’un quadrilatère sont les deux segments dont les extrémités sont deux sommets non consécutifs.
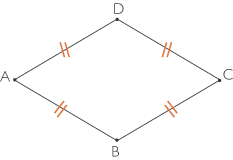
Losange
Définition : un losange est un quadrilatère dont les quatre côtés ont la même longueur.
Propriété
Si un quadrilatère est un losange alors :
ses diagonales sont ses deux axes de symétrie,
ses diagonales sont perpendiculaires,
ses diagonales ont le même milieu,
chaque diagonale est la médiatrice de l’autre,
ses angles opposés sont égaux.
Rectangle
Définition : un rectangle est un quadrilatère qui a quatre angles droits.
Propriété
Si un quadrilatère est un rectangle, alors :
ses diagonales ont la même longueur,
ses diagonales ont le milieu,
ses côtés opposés sont parallèles,
ses côtés opposés ont la même longueur.

Carré
Reconnaître un losange, un carré, un rectangle
Reconnaître un losange : si les diagonales d’un quadrilatère ont le même milieu et sont perpendiculaires, alors ce quadrilatère est un losange.
Reconnaître un rectangle : si un quadrilatère a ses diagonales qui ont le même milieu et qui ont la même longueur, alors ce quadrilatère est un rectangle.
Reconnaître un carré :
Si un losange possède un angle droit, alors c’est un carré.
Si un rectangle possède deux côtés consécutifs de même longueur, alors c’est un carré.
Si les diagonales d’un quadrilatère sont perpendiculaires et si elles ont le même milieu et si elles ont la même longueur, alors ce quadrilatère est un carré.
Définition : un carré est un quadrilatère qui est à la fois un losange et un rectangle.
Propriété : si un quadrilatère est un carré, alors il possède toutes les propriétés du losange et aussi toutes les propriétés du rectangle.

3. Symétrie axiale
Sujet secondaire
Figures symétriques
Définition : deux figures sont symétriques par rapport à une droite (d) si, lorsqu’on plie le long de cette droite (d), elles se superposent exactement.
Exemple : les deux poissons sont symétriques par rapport à la droite (d).
On dit également que :
le poisson 1 est le symétrique du poisson 2 par rapport à la droite (d) ,
le poisson 2 est le symétrique du poisson 1 par rapport à la droite (d) .
Propriété
Le symétrique :
d’une droite est une droite,
d’un segment est un segment de même longueur,
d’un angle est un angle de même mesure,
d’un cercle est un cercle de même rayon.

Axe de symétrie
Définition : on dit qu’une droite (d) est un axe de symétrie d’une figure lorsque cette figure est sa propre symétrique par rapport à la droite (d).
Clique ici pour consulter un exemple.
Propriété : un segment [AB] possède deux axes de symétrie : la droite (AB) et la médiatrice du segment [AB].
De la propriété précédente découle une propriété caractéristique de la médiatrice.
Propriété : l’axe de symétrie d’un angle est sa bissectrice.
Propriété
Si un triangle ABC est isocèle en a, alors :
on a : ABC = ACB se sont des angles
la médiatrice du côté [BC] est un axe de symétrie du triangle. C’est également la bissectrice de l’angle BAC.
Propriété
Si un triangle ABC est équilatéral, alors :
ses trois angles sont égaux,
les médiatrices des trois côtés sont les trois axes de symétrie du triangle. Ce sont également les bissectrices des trois angles.