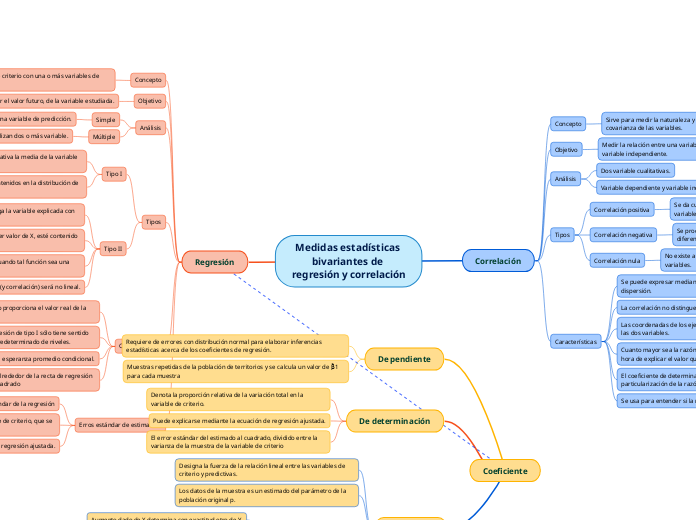
Medidas estadísticas bivariantes de regresión y correlación
Correlación
Concepto
Sirve para medir la naturaleza y grado de relación o covarianza de las variables.
Objetivo
Medir la relación entre una variable dependiente y una variable independiente.
Análisis
Dos variable cualitativas.
Variable dependiente y variable independiente para referirse a las mediciones.
Tipos
Correlación positiva
Se da cuando hay una relación proporcional entre ambas variables.
Correlación negativa
Se produce cuando el comportamiento de una variable es diferente a la otra.
Correlación nula
No existe algún tipo de comportamiento entre ambas variables.
Características
Se puede expresar mediante un diagrama de dispersión.
La correlación no distingue entre variables respuesta
Las coordenadas de los ejes cartesianos se toman las dos variables.
Cuanto mayor sea la razón de correlación mayor será la potencia de X a la hora de explicar el valor que toma Y.
El coeficiente de determinación lineal simple, se denomina así, por ser una particularización de la razón de correlación.
Se usa para entender si la relación es positiva o negativa.
Regresión
Concepto
Relaciona una ecuación con una variable de criterio con una o más variables de predicción.
Objetivo
Construir una función que permita estimar el valor futuro, de la variable estudiada.
Análisis
Simple
Cuando se usa sólo una variable de predicción.
Múltiple
Si se utilizan dos o más variable.
Tipos
Tipo I
Se asigna a cada valor de la variable explicativa la media de la variable explicada condicionada.
Estimaciones de Y para los valores de X contenidos en la distribución de frecuencias.
Tipo II
La función y = f(x) o y = f(x1, x2, …, xp) que liga la variable explicada con la explicativa tiene forma paramétrica
Proporciona estimaciones de Y para cualquier valor de X, esté contenido en la distribución o no.
Así, la regresión (y correlación) será lineal cuando tal función sea una recta, un plano o un hiperplano.
En caso contrario, la regresión (y correlación) será no lineal.
Características
La regresión de una variable sobre otra(s) no proporciona el valor real de la primera.
Si la variable explicativa es cualitativa, la regresión de tipo I sólo tiene sentido cuando dicha variable presenta un número predeterminado de niveles.
Permite calcular una esperanza promedio condicional.
La estimación de la muestra de la varianza alrededor de la recta de regresión se relaciona con la suma de los errores al cuadrado
Erros estándar de estimación
Desviación estándar de la regresión
Valor absoluto de la variación en la variable de criterio, que se deja sin explicación.
No cuenta en la ecuación de regresión ajustada.
Coeficiente
De pendiente
Requiere de errores con distribución normal para elaborar inferencias estadísticas acerca de los coeficientes de regresión.
Muestras repetidas de la población de territorios y se calcula un valor de β̂1 para cada muestra
De determinación
Denota la proporción relativa de la variación total en la variable de criterio.
Puede explicarse mediante la ecuación de regresión ajustada.
El error estándar del estimado al cuadrado, dividido entre la varianza de la muestra de la variable de criterio
Correlación
Designa la fuerza de la relación lineal entre las variables de criterio y predictivas.
Los datos de la muestra es un estimado del parámetro de la población original p.
La correlación positiva perfecta
Aumento dado de X determina con exactitud otro de Y.
Tiene coeficiente +1.
La correlación negativa perfecta
Incremento de X determina exactamente una disminución de Y.
Produce un coeficiente –1.