Modelo de Van Hiele para la
didáctica de la Geometría
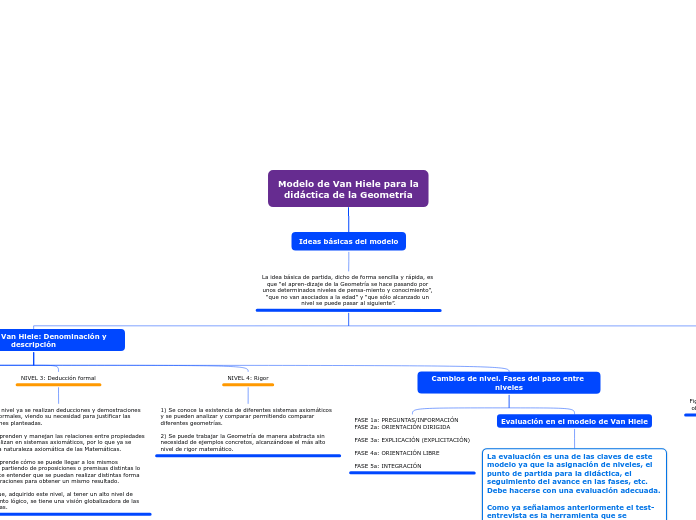
Ideas básicas del modelo
La idea básica de partida, dicho de forma sencilla y rápida, es que “el apren-dizaje de la Geometría se hace pasando por unos determinados niveles de pensa-miento y conocimiento”, “que no van asociados a la edad” y “que sólo alcanzado un nivel se puede pasar al siguiente”.
Niveles de Van Hiele: Denominación y descripción
NIVEL 0: Visualización o reconocimiento
Tres son las características fundamentales de este nivel:
1) Los objetos se perciben en su totalidad como una unidad, sin diferenciar sus atributos y componentes.
2) Se describen por su apariencia física mediante descripciones meramente visuales y asemejándoles a elementos familiares del entorno (parece una rueda, es como una ventana, etc.) No hay lenguaje geométrico básico para llamar a las figuras por su nombre correcto.
3) No reconocen de forma explícita componentes y propiedades de los objetos motivo de trabajo
NIVEL 1: Análisis
1) Se perciben las componentes y propiedades (condiciones necesarias) de los objetos y figuras. Esto lo obtienen tanto desde la observación como de la experimentación.
2) De una manera informal pueden describir las figuras por sus propiedades pero no de relacionar unas propiedades con otras o unas figuras con otras. Como muchas definiciones en Geometría se elaboran a partir de propiedades no pueden elaborar definiciones.
3) Experimentando con figuras u objetos pueden establecer nuevas propiedades
4) Sin embargo no realizan clasificaciones de objetos y figuras a partir de sus propiedades.
NIVEL 2: Ordenación o clasificación
Antes de señalar las características del nivel conviene señalar que, en el anterior nivel, los estudiantes empiezan a generalizar, con lo que inician el razonamiento matemático, señalando qué figuras cumplen una determinada propiedad matemática pero siempre considerará las propiedades como independientes no estableciendo, por tanto, relaciones entre propiedades equivalentes. Alcanzar este nivel significa que...
1) Se describen las figuras de manera formal, es decir, se señalan las condiciones necesarias y suficientes que deben cumplir. Esto es importante pues conlleva entender el significado de las definiciones, su papel dentro de la Geometría y los requisitos que siempre requieren.
2) Realizan clasificaciones lógicas de manera formal ya que el nivel de su razonamiento matemático ya está iniciado. Esto significa que reconocen cómo unas propiedades derivan de otras , estableciendo relaciones entre propiedades y las consecuencias de esas relaciones.
NIVEL 3: Deducción formal
1) En este nivel ya se realizan deducciones y demostraciones lógicas y formales, viendo su necesidad para justificar las proposiciones planteadas.
2) Se comprenden y manejan las relaciones entre propiedades y se formalizan en sistemas axiomáticos, por lo que ya se entiende la naturaleza axiomática de las Matemáticas.
3) Se comprende cómo se puede llegar a los mismos resultados partiendo de proposiciones o premisas distintas lo que permite entender que se puedan realizar distintas forma de demostraciones para obtener un mismo resultado.
Es claro que, adquirido este nivel, al tener un alto nivel de razonamiento lógico, se tiene una visión globalizadora de las Matemáticas.
NIVEL 4: Rigor
1) Se conoce la existencia de diferentes sistemas axiomáticos y se pueden analizar y comparar permitiendo comparar diferentes geometrías.
2) Se puede trabajar la Geometría de manera abstracta sin necesidad de ejemplos concretos, alcanzándose el más alto nivel de rigor matemático.
Cambios de nivel. Fases del paso entre niveles
FASE 1a: PREGUNTAS/INFORMACIÓN
FASE 2a: ORIENTACIÓN DIRIGIDA
FASE 3a: EXPLICACIÓN (EXPLICITACIÓN)
FASE 4a: ORIENTACIÓN LIBRE
FASE 5a: INTEGRACIÓN
Evaluación en el modelo de Van Hiele
La evaluación es una de las claves de este modelo ya que la asignación de niveles, el punto de partida para la didáctica, el seguimiento del avance en las fases, etc. Debe hacerse con una evaluación adecuada.
Como ya señalamos anteriormente el test-entrevista es la herramienta que se considera más útil para realizarla y, para ello se deben tener en cuenta algunas ideas previas, así apuntamos que...
1. El nivel de razonamiento de los alumnos depende del área de las Matemáticas que se trate.
2. Se debe evaluar cómo los alumnos contestan y el por qué de sus respuestas, más que lo que no contestan o contestan bien o mal.
3. En las preguntas no está el nivel de los alumnos/as sino que está en sus respuestas.
4. En unos contenidos se puede estar en un nivel y, en otros diferentes, en nivel distinto.
5. Cuando se encuentran en el paso de un nivel a otro puede resultar difícil determinar la situación real en que se encuentran.
Características de los niveles
NIVEL 0
Figuras y objetos Partes y propiedades de las figuras y
objetos
NIVEL 1
Partes y propiedades de las figuras y objetos
Implicaciones entre propiedades de figuras y objetos
NIVEL 2
Implicaciones entre propiedades
de figuras y objetos
Deducción formal de teoremas
NIVEL 3
Deducción formal de teoremas Relación entre los teoremas (sistemas axiomáticos)