
Классификация систем счисления
Непозиционные системы счисления
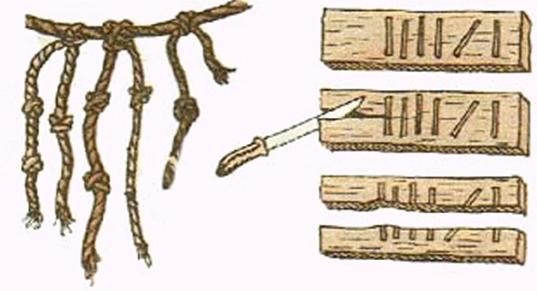
Единичная
(унарная)
Интересный факт:
Мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.
Основные недостатки:
1. Запись больших чисел требует введения новых символов.
2. Невозможно представлять дробные и отрицательные числа.
3. Сложно выполнять простейшие арифметические операции, так как не существует алгоритмов их выполнения.

Египетская

Древнегреческая

Славянская
кириллическая

Римская
Позиционные системы счисления

Двоичная:
используются всего 2е цифры - 0 и 1.
(применяется в ЭВМ)

Двадцатиричная (система счёта Майя):
Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять). Число 20 изображалось из двух цифр, ноль и один наверху и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие. Если число ноль появлялось без единицы наверху, то это обозначало, что единиц данного разряда нет.
Важно знать:
Основанием позиционной системы счисления может быть любое число, большее1. Основание системы приписывается нижним индексом к этому числу.
Основные преимущества:
1. Для записи больших чисел применяется небольшое количество цифр.
2. Удобно производить арифметические операции.

Вавилонская (десятеричная / шестидесятеричная):
В этой системе числа менее 60 обозначались с помощью двух знаков. Числа больше 60 записывались по разрядам, с небольшими пробелами между ними.
1*60*60+2*60+5 = 3725
2*60*60+3 = 7203

Восьмиричная:
используются цифры -
0, 1, 2, 3, 4, 5, 6, 7.
Шведский король Карл ХII в 1717 году увлекся этой системой и собирался ввести её как общегосударственную.

Двенадцатиричная:
используются следующие символы -
0,1,2,3,4,5,6,7,8,9,A,B.
Число двенадцать (дюжина) даже составляла конкуренцию десятке в борьбе за статус общеупотребительной системы счисления. Дело
в том, что число 12 имеет больше делителей(2,3,4,6), чем 10(2,5). Поэтому
в 12-ричной системе гораздо удобнее производить расчёты, нежели в десятичной.
Дюжина очень прочно вошла в нашу жизнь (например, многие предметы продаются дюжинами).

Десятиричная:
Самая распространённая в мире система счисления.
«Преимущество десятичной системы не математическое,
а зоологическое. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой» (Н.Н. Лузин)
