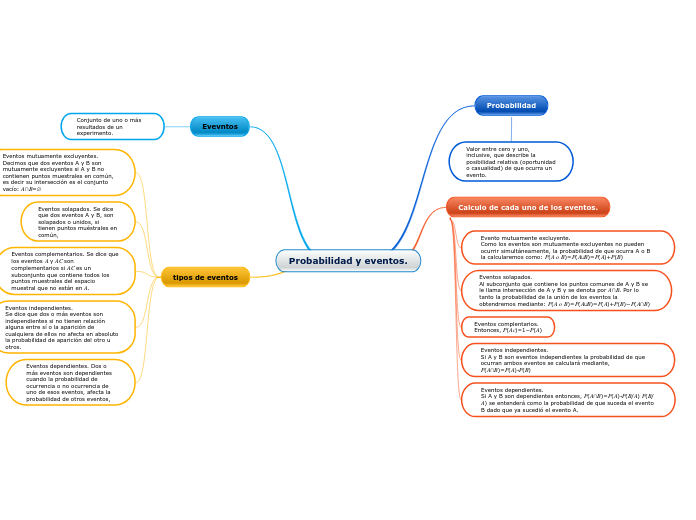
Probabilidad y eventos.

Probabilidad

Valor entre cero y uno, inclusive, que describe la posibilidad relativa (oportunidad o casualidad) de que ocurra un evento.

Calculo de cada uno de los eventos.

Evento mutuamente excluyente.
Como los eventos son mutuamente excluyentes no pueden ocurrir simultáneamente, la probabilidad de que ocurra A o B la calcularemos como: 𝑃(𝐴 𝑜 𝐵)=𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)

Eventos solapados.
Al subconjunto que contiene los puntos comunes de A y B se le llama intersección de A y B y se denota por 𝐴∩𝐵. Por lo tanto la probabilidad de la unión de los eventos la obtendremos mediante: 𝑃(𝐴 𝑜 𝐵)=𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵)

Eventos complentarios.
Entonces, 𝑃(𝐴𝑐)=1−𝑃(𝐴)

Eventos independientes.
Si A y B son eventos independientes la probabilidad de que ocurran ambos eventos se calculará mediante, 𝑃(𝐴∩𝐵)=𝑃(𝐴)∗𝑃(𝐵)

Eventos dependientes.
Si A y B son dependientes entonces, 𝑃(𝐴∩𝐵)=𝑃(𝐴)∗𝑃(𝐵/𝐴) 𝑃(𝐵/𝐴) se entenderá como la probabilidad de que suceda el evento B dado que ya sucedió el evento A.

Evevntos

Conjunto de uno o más resultados de un experimento.

tipos de eventos

Eventos mutuamente excluyentes. Decimos que dos eventos A y B son mutuamente excluyentes si A y B no contienen puntos muestrales en común, es decir su intersección es el conjunto vacío: 𝐴∩𝐵=∅

Eventos solapados. Se dice que dos eventos A y B, son solapados o unidos, si tienen puntos muéstrales en común,

Eventos complementarios. Se dice que los eventos 𝐴 y 𝐴𝐶 son complementarios si 𝐴𝐶 es un subconjunto que contiene todos los puntos muestrales del espacio muestral que no están en 𝐴.

Eventos independientes.
Se dice que dos o más eventos son independientes si no tienen relación alguna entre sí o la aparición de cualquiera de ellos no afecta en absoluto la probabilidad de aparición del otro u otros.

Eventos dependientes. Dos o más eventos son dependientes cuando la probabilidad de ocurrencia o no ocurrencia de uno de esos eventos, afecta la probabilidad de otros eventos,