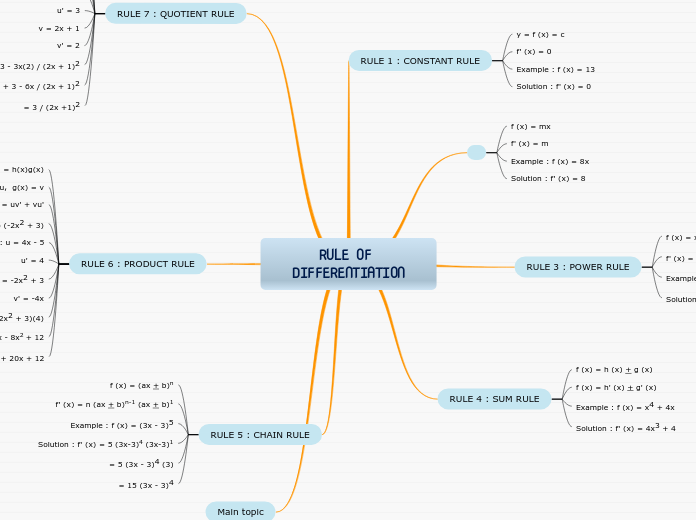
RULE OF DIFFERENTIATION

y = f (x) = c

f' (x) = 0

Example : f (x) = 13

Solution : f' (x) = 0

f (x) = mx

f' (x) = m

Example : f (x) = 8x

Solution : f' (x) = 8

f (x) = xn

f' (x) = nxn-1

Example : x9

Solution : 9x8

f (x) = h (x) + g (x)

f (x) = h' (x) + g' (x)

Example : f (x) = x4 + 4x

Solution : f' (x) = 4x3 + 4

f (x) = h(x) / g(x)

h(x) = u, g(x)

f'(x) = vu' - uv' / v2

Example : 3x / 2x + 1

Solution : u = 3x

u' = 3

v = 2x + 1

v' = 2

f' (x) = (2x + 1)3 - 3x(2) / (2x + 1)2

= 6x + 3 - 6x / (2x + 1)2

= 3 / (2x +1)2

f (x) = h(x)g(x)

h(x) = u, g(x) = v

f' (x) = uv' + vu'

Example : (4x - 5) (-2x2 + 3)

Solution : u = 4x - 5

u' = 4

v = -2x2 + 3

v' = -4x

f' (x) = (4x - 5)(-4x) + (-2x2 + 3)(4)

= -16x2 + 20x - 8x2 + 12

= -24x2 + 20x + 12

f (x) = (ax + b)n

f' (x) = n (ax + b)n-1 (ax + b)1

Example : f (x) = (3x - 3)5

Solution : f' (x) = 5 (3x-3)4 (3x-3)1

= 5 (3x - 3)4 (3)

= 15 (3x - 3)4