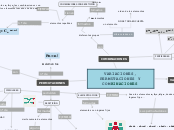
VARIACIONES, PERMUTACIONES Y COMBINACIONES
VARIACIONES
dieferentes grupos
m elementos
n en n
diferenciados en
en un elemento
ab - ac - bc
orden de los elementos
ba - ca - cb
6 variaciones
Vn=m! / (m-n)!
PERMUTACIONES
ELEMENTOS FIJOS
elementos con lugares fijos

Sean los elementos a, b, c, d y e, donde a y b ocupan lugares fijos...
abcde - abced - abecd - abedc - abdac - abdca
diferentes grupos
todos los elementos de un conjunto
orden de los elementos
Sean los elementos a, b y c...
abc - bac - bca cab - cba

REPETICIÓN
cierto numero de elementos
son iguales
nª de permutaciones
n elementos
Px; y; z= n!/x!xy!xz!
n

Sean los elementos a, que se repite 3 veces, y b que se repeite 2 veces...
aaabb - aabab - aabba - abaab - ababa - abbaa - baaab - baaba - babaa - bbaaa
CIRCULARES
sobre una línea cerrada NO HAY:
primer elemento
ultimo elemento

n elementos
PCn=(n-1)!
n elementos
Pn=n!
COMBINACIONES
dieferentes grupos
m elementos
n en n
COMBINACIONES CON REPETICIÓN
elementos repetidos
Sean los elementos a, b y c, las combinaciones con repetición de estos elementos tomados de dos en dos serán...
aa - ab - ac - bb - bc - cc
6 combinaciones
CRmn= Cn m+n-1
diferenciados en
un elemento
NO SE TOMA EN CUENTA
orden de los elementos
PROPIEDADES
Cmn+Cmn+1 = Cm+1n+1
Cmn = (m/n)Cm-1n-1
Cmn = Cmm-n
Cmn=Cmp
n=p v n+p=m