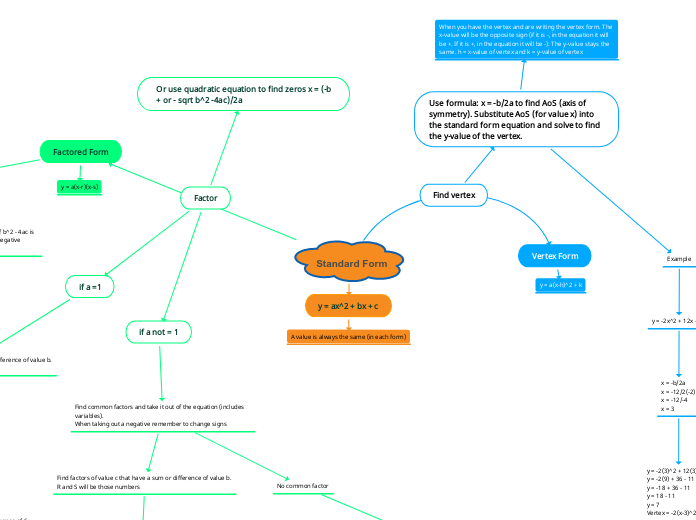
Standard Form
Factored Form
y = a(x-r)(x-s)
Special cases
When using the quadratic equation, if the result of b^2 - 4ac is negative, then there are no zeros (cannot sqrt a negative number!). This means there is no factored form.
y = ax^2 + bx + c
A value is always the same (in each form)
Vertex Form
y = a(x-h)^2 + k
Find vertex
Use formula: x = -b/2a to find AoS (axis of symmetry). Substitute AoS (for value x) into the standard form equation and solve to find the y-value of the vertex.
Example
y = -2x^2 + 12x - 11
x = -b/2a
x = -12/2(-2)
x = -12/-4
x = 3
y = -2(3)^2 + 12(3) - 11
y = -2(9) + 36 - 11
y = -18 + 36 - 11
y = 18 - 11
y = 7
Vertex = -2(x-3)^2 + 7
substitude AoS into equation for x to find y-value of vertex
When you have the vertex and are writing the vertex form. The x-value will be the opposite sign (if it is -, in the equation it will be +. If it is +, in the equation it will be -). The y-value stays the same. h = x-value of vertex and k = y-value of vertex
Factor
if a not = 1
Find common factors and take it out of the equation (includes variables).
When taking out a negative remember to change signs
Find factors of value c that have a sum or difference of value b.
R and S will be those numbers
Example
y = -2x^2 + 14x - 24
Common factor of 2 (-2 so change signs)
y = -2(x^2 - 7x + 12)
Find factors of 12 that have a sum or difference of -7
12 = (-3)x(-4)
-7 = -3-4
Therefore y = -2(x-3)(x-4)
No common factor
Multiply value a with value c. Find factors of the product that have a sum or difference of value b. With those 2 factors, replace value b. Common factor the 1st 2 terms then the last 2 terms.
Example
y = 4x^2 + 7x + 3
4x3 = 12
7 = 3+4
y = 4x^2 + 3x + 4x + 3
y = x(4x + 3)+ 1(4x+3)
therefore factored form is
y = (x+1)(4x+3)
if a =1
Find factors of value c that have a sum or difference of value b.
R and s will be those two numbers
Example
y = x^2 + 6x + 8
a = 1
Find factors of 8 that have a sum or difference of 6
8 = 2x4
6 = 2+ 4
Therefore y = (x+2)(x+4)
Or use quadratic equation to find zeros x = (-b + or - sqrt b^2 -4ac)/2a
Special occasions
When the two factors are the same number
there is only 1 x-int
Example
y = x^2 + 10x + 25
25 = 5x5
5+5 = 10
y = (x+5)(x+5)
y = (x+5)^2