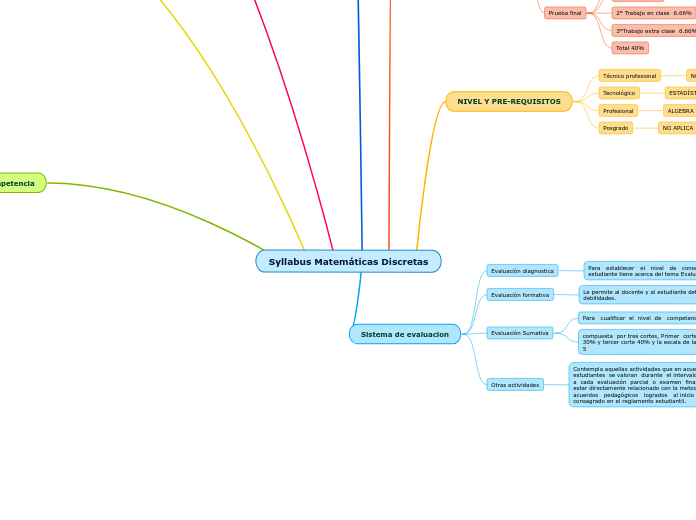
Syllabus Matemáticas Discretas

Programa académico al que corresponde la asignatura

CIENCIAS BASICAS

Programa o area que oferta la asignatura

CENCIAS BASICAS

Correo electrónico del programa o área que oferta a la asignatura

Area_Matematica@cun.edu.co

Prueba parcial 1

Evaluación principal: 15%

1º Quiz: 5%

2º Trabajo en clase 5%

3ºTrabajo extra clase 5%

Total 30%

Prueba parcial 2

Evaluación principal: 15%

1º Quiz: 5%

2º Trabajo en clase 5%

3ºTrabajo extra clase 5%

Total 30%

Prueba final

Evaluación principal: 20%

1º Quiz: 6.66%

2º Trabajo en clase 6.66%

3ºTrabajo extra clase 6.66%

Total 40%

Técnico profesional

NO APLICA

Tecnológico

ESTADÍSTICA DE LA PROBABILIDAD

Profesional

ALGEBRA MODERNA

Posgrado

NO APLICA

Evaluación diagnostica

Para establecer el nivel de conocimientos que el estudiante tiene acerca del tema Evaluación

Evaluación formativa

Le permite al docente y al estudiante detectar las fortalezas y debilidades.

Evaluación Sumativa

Para cualificar el nivel de competencias y está

compuesta por tres cortes, Primer corte 30%, segundo corte 30% y tercer corte 40% y la escala de las mismas es de 0.1 a 5

Otras actividades

Contempla aquellas actividades que en acuerdo con los estudiantes se valoran durante el intervalo de tiempo previo a cada evaluación parcial o examen final Lo anterior debe estar directamente relacionado con la metodología, los acuerdos pedagógicos logrados al inicio del curso y lo consagrado en el reglamento estudiantil.

Hora de trabajo directo con el docente: 48 horas

Codigo: SIA 93736

Nro. Créditos: 3

Nombre Asig: MATEMATICAS DISCRETAS

Academico

El docente que imparta la asignatura puede ser un

● profesional con formación disciplinar en Ingenierías y/o Licenciado en Matemáticas y Física.

● con conocimientos y experiencia reconocida en la enseñanza de ella.

Experiencia

Experiencia mínima de 3 años en educación superior

Observaciones

no

La MATEMATICA DISCRETA Proporciona al estudiante las herramientas y métodos teóricos de las Matemáticas que le permitan visualizar el desarrollo tanto académico como profesional relacionado con las ingenierías

problemas, propósito de formacion

¿Cómo diseñar un algoritmo para calcular todos los factores primos de un número compuesto mediante un segundo lenguaje que sirva de base para crear un programa de ordenador?

¿Cómo Generar algoritmos para calcular diferentes tipos de permutaciones, combinaciones y el teorema del binomio de Newton, diseñe un software que lo ejecute?

¿Cómo utilizar el algoritmo de Moore para determinar la distancia entre dos vértices de un mismo grafo?

Competencias

El Área de Ciencias Básicas tiene como búsqueda primordial:

Desarrollar en el alumno la capacidad analítica, lógica, interpretativa y creativa en la resolución de problemas matemáticos, orientándolos a un contexto especifico a través de hábitos de consulta e investigación en los estudiantes que proporcionen la formación profesional adecuada para las necesidades del mundo laboral; y los retos organizativos y de gestión que tiene planteado nuestra sociedad actual.

COMPETENCIA DEL ÁREA PARA EL CICLO PROFESIONAL

Modela situaciones problemas determinando técnicas de solución basadas en teorías matemáticas usadas en la toma de decisiones.

COMPETENCIA ACADÉMICA DE LA ASIGNATURA:

Diseña y crea una página, como proyecto final de la asignatura, en la cual se dinamicen los programas creados en el semestre.

El estudiante estará en capacidad de reconocer la evolución de las matemáticas discretas y su importancia para las ciencias de la computación.

El estudiante podrá interpretar las distintas herramientas teóricas empleadas por los algoritmos que resuelven problemáticas de las teorías de grafos, arboles, autómatas y números, en el campo de las matemáticas discretas.

El estudiante estará en capacidad de plantear la construcción de algoritmos y modelos matemáticos que conceptualicen las variables, los parámetros y las relaciones conjuntistas de los problemas propios de las matemáticas discretas.