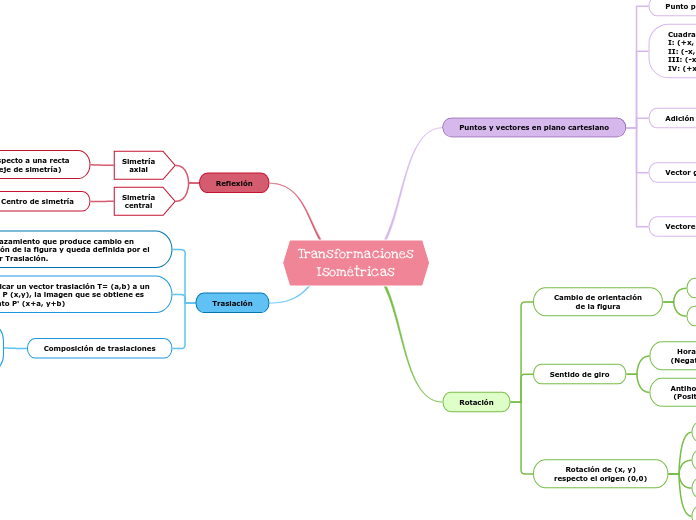
Transformaciones
Isométricas
Puntos y vectores en plano cartesiano
Punto plano cartesiano: (x,y)
Cuadrantes del plano:
I: (+x, +y)
II: (-x, +y)
III: (-x, -y)
IV: (+x, -y)
Adición de vectores
Ley del triángulo
Si punto de llegada de uno de los vectores coincide con el punto de inicio del otro.
Ley del paralelogramo
Si vectores tiene punto de partida en común
Vector geométrico
Tiene punto inicial(u origen), punto final, dirección, sentido y magnitud
Vectores equipolentes
Igual dirección, sentido y magnitud
A (x₁,y₁), B (x₂, y₂) Vector AB (x₂-x₁, y₂-y₁)
Rotación
Cambio de orientación
de la figura
Centro de rotación
Ángulo de giro
Sentido de giro
Horaria
(Negativa)
R (P, -a)
Antihoraria
(Positiva)
R (P, a)
Rotación de (x, y)
respecto el origen (0,0)
Giro 90º
(-y, x)
Giro 180º
(-x, -y)
Giro 270º
(y, -x)
Giro 360º
(x, y)
Reflexión
Simetría
axial
Respecto a una recta
(eje de simetría)
Simetría
central
Respecto a punto : Centro de simetría
Traslación
Desplazamiento que produce cambio en posición de la figura y queda definida por el Vector Traslación.
Al aplicar un vector traslación T= (a,b) a un punto P (x,y), la imagen que se obtiene es el punto P' (x+a, y+b)
Composición de traslaciones
Se puede reducir a una única traslación cuyo vector de traslación corresponde a la suma de cada vector por separado: Vector T (a,b) o Vector T' (c,d) = Vector T'' (a+c, b+d)