Vias para la demostracion de un Teorema
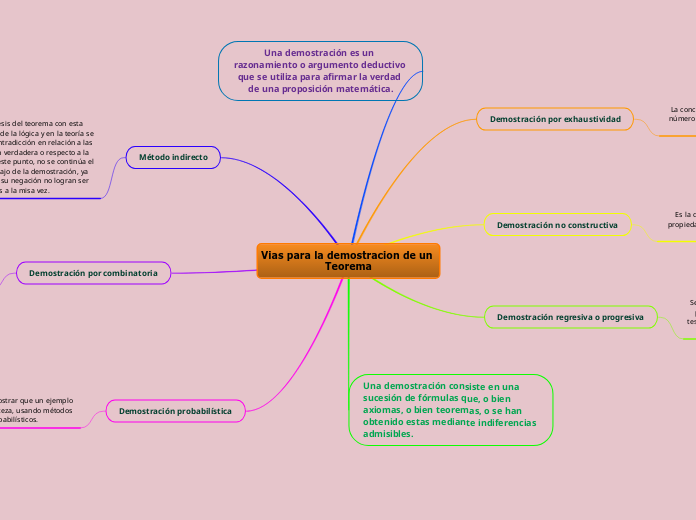
Una demostración es un razonamiento o argumento deductivo que se utiliza para afirmar la verdad de una proposición matemática.
Método indirecto
Radica en negar la tesis del teorema con esta proposición y las reglas de la lógica y en la teoría se tiene que hallar una contradicción en relación a las premisas, una posición verdadera o respecto a la suposición. A partir de este punto, no se continúa el procedimiento de trabajo de la demostración, ya que una proposición y su negación no logran ser verdaderas a la misa vez.
Demostración por combinatoria
La misma establece la igualdad de expresiones desiguales al mostrar que cuentas para el mismo objeto.
Demostración probabilística
Consiste en mostrar que un ejemplo existe, con certeza, usando métodos probabilísticos.
Demostración por exhaustividad
La conclusión se sustituye al fraccionarla en un número finito de casos y experimentar cada uno por individual.
Demostración no constructiva
Es la que determina que un objeto con una propiedad existe sin explicar cómo tal objeto se puede encontrar.
Demostración regresiva o progresiva
Se combina con otros métodos, se caracteriza por partir de la hipótesis y llegar directamente a la tesis o conclusión, o puede partir de la conclusión y llegar a la hipótesis.