บรรณานุกรม
ออนไลน์
หนังสือ
สวนศาสตร์ทางดนตรี
Musical acoustics
Instrument Acoustics
Percussion
Brass
Slide
Bb
BBb
Woodwind
ท่อขยาย
ท่อตรง
String
ระบบเสียงและการวัดเสียง
Cent
Subtopic
Tuning system
Equal temperament
Just intonation
Pythagorean tuning system
Temperament Problem
Temperament Problems
For over two centuries the predominant musical scale used, at least for western music, has been the equal tempered
scale. The ability to freely modulate between musical keys and the equivalence of all musical keys were strong enough features to overcome reservations about the compromises made with the small-integer-ratio
rule. The kinds of problems which led to this compromise scale were:

The Whole Tone
In the buildup of a pentatonic scale
using the musical intervals
which have been found to be universally consonant ( octave, fifth, and fourth), an interval of ratio 9/8 naturally emerges. This interval satisfies the basic condition for consonance
and it occurs in the basic pentatonic scale. This suggests the carving of another such whole tone from the larger interval remaining, leaving the smaller 256/243 interval. This whole tone is used in the Just
and Pythagorean
temperaments. In devising the equal tempered
scale it was important to maintain not only the octave, fifth, and fourth at close to their just values, but also to maintain the whole tone. Expressed in cents
notation, the natural whole tone is 204¢, compared to 200¢ for the equal tempered whole tone, just within the accepted 5¢ just noticeable difference
.
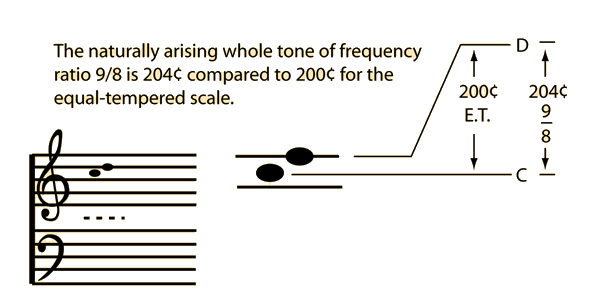
The natural wholle tone that arises in Pythagorean temperament leads to certain difficulties
when compared to equal temperament as shown below.
pythagorean interval
Pythagorean Intervals
The Pythagorean
temperament produces two different semitones. When expressed in cents
, it becomes evident that their differences are well above the just noticeable difference
in pitch.

This leads to certain difficulties
which ultimately led to the development of equal temperament
.
pythagorean tuning
Pythagorean Temperament
A pentatonic
musical scale can be devised with the use of only the octave, fifth and fourth. It produces three intervals
with ratio 9/8 and two larger intervals. If a 9/8 (whole tone
) interval is carved out of the larger ones, a smaller (semitone) interval is left: B-C and E-F. This creates a Pythagorean diatonic scale
. If the semitone thus created is taken from the whole tone, a chromatic semitone
of different size is left over. This leads to some of the difficulties
of Pythagorean temperament and other temperaments - such difficulties ultimately led to the development of equal temperament
.
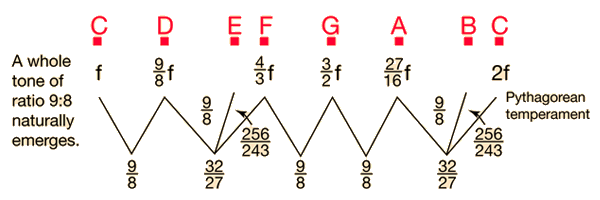
The use of the octave and the fifth (ratio 3:2) is attributed to Pythagorus in the sixth century BC.
การเกิดเสียงและคุณสมบัติของเสียง
การเคลื่อนที่, แรง, พลังงาน
1. การเคลื่อนที่, แรง, พลังงาน
การหาระยะทางโดยทั่วไป ถ้ามีคนถามว่าขณะนี้คุณอยู่ตรงไหน แล้วเราบอกว่า อยู่ทางเหนือของมหาวิทยาลัย 2 กิโลเมตร การคาดเดาทำให้ยากเพราะด้านเหนือของมหาวิทยาลัยถ้าวัดโดยใช้จุดมหาวิทยาลัยเป็นจุดตั้งต้น เราไม่สามารถกำหนดของจุดที่อยู่ได้อย่างชัดเจน แต่ถ้าบอกเพิ่มอีกว่า อยู่ทางตะวันออก 2.5 กิโลเมตร เราสามารถกำหนดจุดตำแหน่งได้อย่างชัดเจน ดังภาพ
จุดที่เป็นเส้นตัดกัน (A) สามารถบอกระยะตำแหน่งของสถานที่ ที่ต้องการได้ การหาระยะและตำแหน่งทิศเหนือและทิศตะวันออกดังกล่าว ใช้การแทนค่าโดยแกน X และ Y โดยแกน X แทนค่าทิศ เหนือ, ใต้ ส่วนแกน Y แทนค่า ทิศตะวันออก,ตะวันตก
การหาระยะทาง หรือ Distance, speed and velocity ของเสียงใช้การหาดังนี้
Distance = Speed x Time
Speed =
นักฟิสิกส์มักใช้ velocity มากกว่า Speed , velocity ให้ความหมายถึงการคลื่นไหวโดยตรงได้ดีกว่า speed
Sine – wave เป็นคลื่นเสียงพื้นฐาน
เสียงใด ๆ ที่ซับซ้อน"สามารถอธิบายเป็นการรวมกันของคลื่นเป็นระยะ ๆ หลายอย่างง่าย (เช่น คลื่นไซน์ ) หรือ partials แต่ละส่วน มีความถี่ของจากการสั่นสะเทือนของคลื่น Amplitude and Phase
Patial คือส่วนหนึ่งของคลื่น sine wave คลื่นไซน์ ที่รวมกันเป็นเสียงที่ซับซ้อนขึ้น
A harmonic (or a harmonic partial) ชุดย่อยของ Patial เสียงที่เกิดจากการสั่นสะเทือน ที่มีการคูณจำนวนทั้งหมดของเสียงตั้งแต่ความถี่พื้นฐาน จนถึงหางเสียงสุดท้าย
Inharmonicity เป็นตัวชี้วัดของส่วนเบี่ยงเบน จากเสียงที่ใกล้ที่สุดที่ ในฮาร์โมนิกของเสียง โดยแสดงค่าเบี่ยงเบนเป็น Cent
โดยทั่วไปแล้ว ระดับเสียง (pitch) ของเครื่องดนตรี จะมี partials ที่อยู่ใกล้กับเสียง เริ่มต้นของ Harmonic ด้วยเสียงที่ต่ำ ยกเว้นเครื่องดนตรีบางชนิดที่จัดอยู่ในประเภท Inharmonic เช่นเครื่องประเภท Percussion ต่าง ๆ เช่น Marimba, Vibraphone, Tubular bell และ Timpani ประกอบด้วยกลุ่มเสียง Non Harmonics แต่ยังให้ความรู้สึกที่ดีในการฟังแต่ในกลุ่มที่เป็น Non Pitch เช่น Cymbals, Gong, Tam tams สร้างเสียงใน Inharmonic มาก
Overtone คือกลุ่มเสียง Patial อื่น ๆ ที่นอกเหนือจากเสียงต่ำ Overtone ไม่ได้หมายความถึง harmonicas หรือ inharmonicity และไม่ได้หมายถึง เสียงพื้นฐาน (Fundamental) ด้วย เครื่องดนตรี Electronic สามารถสร้างความถี่เสียงโดยไม่มี Overtone ได้ และสามารถผสมผสานความถี่ Overtone เข้ามาในความถี่เสียงหลักได้ ลักษณะเช่นนี้ทำให้เกิด Timber ของเสียง
Timber สีสันของเสียงเกิดจาก Overtone ที่มีความดังหรือ Amplitude แตกต่างกันทำให้เกิดความดังของเสียงใน Overtone ที่แตกต่างกัน
Speed of Sound in Air
Speed of Sound in Air
The speed of sound in dry air is given approximately by
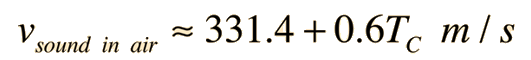
for temperatures reasonably close to room temperaature, where TC is the celsius temperature
,
so that at temperature C = F,
the speed of sound is m/s = ft/s = mi/hr.
This calculation is usually accurate enough for dry air, but for great precision one must examine the more general relationship for sound speed in gases
. If you measured sound speed in your oven, you would find that this relationship doesn't fit. At 200°C this relationship gives 453 m/s while the more accurate formula gives 436 m/s. This sound speed does not apply to gases other than air, for example the helium
from a balloon.
It is important to note that the sound speed in air is determined by the air itself. It is not dependent upon the sound amplitude, frequency or wavelength.
Calculation note: You may enter temperature to calculate sound speed, or enter sound speed to calculate the corresponding temperature.
V = Speed of sound + (0.6)* Temperature
ความเร็วเสียง = 331.4 + (0.6)* อุณหภูมิ ในอากาศ
เมตร / วินาที
ตัวอย่างเช่น ความเร็วเสียงที่อุณหภูมิ 25 องศาเซลเซียสได้เท่ากับ
331.4+(0.6)*25 = 346.4 เมตร / วินาที
ความเร็วเสียงที่อุณหภูมิ 10 องศาเซลเซียสเท่ากับ
331.4 + (0.6)*10 = 337.4 เมตร / วินาที
สรุปได้ว่า เสียงจะเดินทางได้เร็วขึ้น เมื่ออุณหภูมิสูงขึ้น เสียงจะเดินทางช้าลงเมื่ออุณหภูมิต่ำลง
สิ่งสำคัญคือต้องสังเกตว่าความเร็วเสียงในอากาศจะถูกกำหนดโดยอากาศเอง ไม่ขึ้นอยู่กับความกว้างคลื่นความถี่หรือความยาวคลื่นของเสียง
ถ้าคุณวัดความเร็วเสียงในเตาอบของคุณคุณจะพบว่าความสัมพันธ์นี้เท่ากัน 200 ° C ความสัมพันธ์นี้จะให้ 453 m / s ในขณะที่สูตรที่แม่นยำยิ่งขึ้นให้ 436 m / s ความเร็วเสียงนี้ใช้ไม่ได้กับแก๊สอื่นที่ไม่ใช่อากาศเช่นฮีเลียม ฉนั้น ความเร็วเสียงที่แตกต่างกัน ขึ้นอยู่กับ ตัวนำเสียงและอุณหภูมิของตัวนำเสียง
การคำนวณนี้มักจะมีความถูกต้องเพียงพอสำหรับอากาศแห้ง แต่สำหรับความแม่นยำที่ดีเราต้องตรวจสอบความสัมพันธ์ทั่วไปสำหรับความเร็วของเสียงในก๊าซ
ความเร็วของเสียงในอากาศ จะได้ใกล้เคียงกับอุณหภูมิห้องที่ TC มีอุณหภูมิเซลเซียส
ความเร็วเสียงในอากาศ
Diffraction of Sound
Diffraction of Sound
Diffraction: the bending of waves around small* obstacles and the spreading out of waves beyond small* openings.
* small compared to the wavelength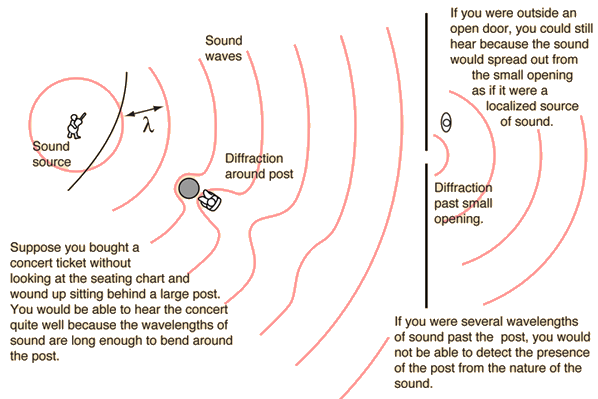
Important parts of our experience with sound involve diffraction. The fact that you can hear sounds around corners and around barriers involves both diffraction and reflection of sound. Diffraction in such cases helps the sound to "bend around" the obstacles. The fact that diffraction is more pronounced with longer wavelengths implies that you can hear low frequencies around obstacles better than high frequencies, as illustrated by the example of a marching band
on the street. Another common example of diffraction is the contrast in sound from a close lightning strike and a distant one. The thunder from a close bolt of lightning will be experienced as a sharp crack, indicating the presence of a lot of high frequency sound. The thunder from a distant strike will be experienced as a low rumble since it is the long wavelengths which can bend around obstacles to get to you. There are other factors such as the higher air absorption of high frequencies involved, but diffraction plays a part in the experience.
You may perceive diffraction to have a dual nature, since the same phenomenon which causes waves to bend around obstacles causes them to spread out past small openings. This aspect of diffraction also has many implications. Besides being able to hear the sound when you are outside the door as in the illustration above, this spreading out of sound waves has consequences when you are trying to soundproof a room. Good soundproofing requires that a room be well sealed, because any openings will allow sound from the outside to spread out in the room - it is surprising how much sound can get in through a small opening. Good sealing of loudspeaker cabinets is required for similar reasons.
Another implication of diffraction is the fact that a wave which is much longer than the size of an obstacle, like the post in the auditorium above, cannot give you information about that obstacle. A fundamental principle of imaging is that you cannot see an object which is smaller than the wavelength of the wave with which you view it. You cannot see a virus with a light microscope because the virus is smaller than the wavelength of visible light. The reason for that limitation can be visualized with the auditorium example: the sound waves bend in and reconstruct the wavefront past the post. When you are several sound wavelengths past the post, nothing about the wave gives you information about the post. So your experience with sound can give you insights into the limitations of all kinds of imaging processes.
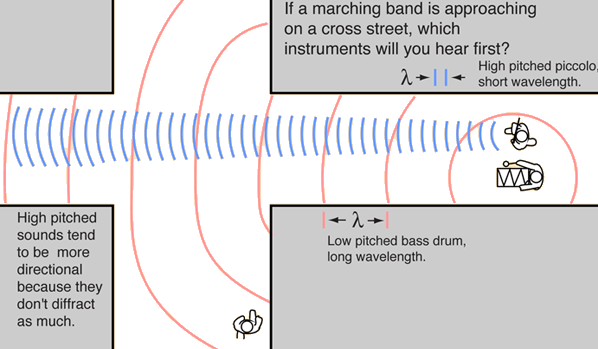
The long wavelength sounds of the bass drum will diffract
around the corner more efficiently than the more directional, short wavelength sounds of the higher pitched instruments.
Loudspeaker Sound Contours
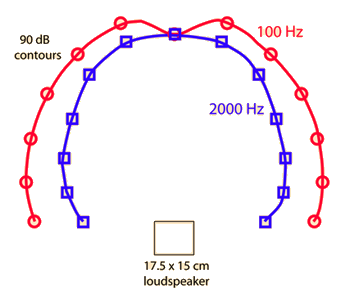 One consequence of diffraction
One consequence of diffraction
is that sound from a loudspeaker
will spread out rather than just going straight ahead. Since the bass frequencies have longer wavelengths compared to the size of the loudspeaker, they will spread out more than the high frequencies. The curves at left represent equal intensity
contours at 90 decibels
for sound produced by a small enclosed loudspeaker. It is evident that the high frequency sound spreads out less than the low frequency sound.
These equal intensity curves were measured in an undergraduate sound laboratory experiment.
Note that the wavelength
of the 100 Hz sound is about 3.45 meters, much larger than the speaker, while that of the 2000 Hz sound is about 18 cm, about the size of the speaker.
The realities of diffraction may affect your choice of loudspeakers for your personal listening. Very small loudspeakers are often promoted as having sound just as good as a large loudspeaker. There is reason to be skeptical about such claims on physical grounds. Large speakers are inherently more efficient in producing bass frequencies into a room just because their size compares more favorably with the wavelengths
of those sounds. Even if that basic problem is overcome by electronic equalization of the sound input to the speakers and the design of the crossover networks
which provide the signal to the different components
of the loudspeaker, there is no escaping the implications of diffraction. Small loudspeakers will spread the bass frequencies considerably more than the high frequencies. This difference between the equal-loudness patterns of highs and lows becomes more and more pronounced as you produce smaller and smaller speakers. So you might conceivably get equivalent sound directly on-axis with the speaker, but as you move away from the axis, the high frequencies will drop off more rapidly than the lows. Practically, this limits the audience region for optimal listening. It might be fairly said that if the speakers are just for you, you might be satisfied with the small speakers because you can position yourself at the ideal-listener location. But if you have guests, they will not be as satisfied because of the greater off-axis variations from the small speakers.
Refraction of Sound
Refraction of Sound
Refraction is the bending of waves when they enter a medium where their speed is different. Refraction is not so important a phenomenon with sound as it is with light where it is responsible for image formation by lenses, the eye, cameras, etc. But bending of sound waves does occur and is an interesting phenomena in sound
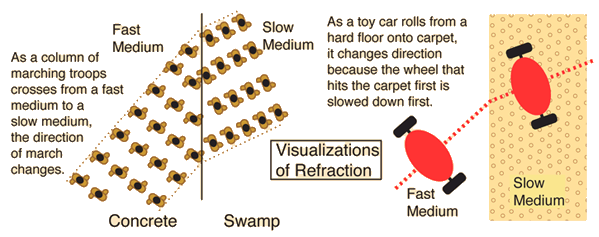
These visualizations may help in understanding the nature of refraction. A column of troops approaching a medium where their speed is slower as shown will turn toward the right because the right side of the column hits the slow medium first and is therefore slowed down. The marchers on the left, perhaps oblivious to the plight of their companions, continue to march ahead full speed until they hit the slow medium.
Not only does the direction of march change, the separation of the marchers is decreased. When applied to waves, this implies that the direction of propagation of the wave is deflected toward the right and that the wavelength of the wave is decreased. From the basic wave relationship, v=fλ , it is clear that a slower speed must shorten the wavelength since the frequency of the wave is determined by its source and does not change.
Another visualization of refraction can come from the steering of various types of tractors, construction equipment, tanks and other tracked vehicle. If you apply the right brake, the vehicle turns right because you have slowed down one side of the vehicle without slowing down the other.
Refraction of Sound
If the air above the earth is warmer than that at the surface, sound will be bent back downward toward the surface by refraction.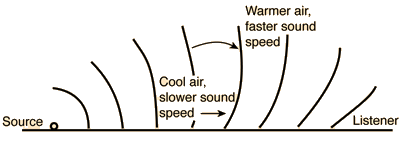 Sound propagates in all directions from a point source. Normally, only that which is initially directed toward the listener can be heard, but refraction can bend sound downward. Normally, only the direct sound is received. But refraction can add some additional sound, effectively amplifying the sound. Natural amplifiers can occur over cool lakes.
Sound propagates in all directions from a point source. Normally, only that which is initially directed toward the listener can be heard, but refraction can bend sound downward. Normally, only the direct sound is received. But refraction can add some additional sound, effectively amplifying the sound. Natural amplifiers can occur over cool lakes.

Refraction of Sound
Early morning fishermen may be the persons most familiar with the refraction of sound. Consider that you have gone out to a lake before dawn. Just as the sun rises over a cool lake, you may hear someone speak to you, saying "Good morning!". You look around and can't see anyone. You are just about at the point of questioning your sanity anyway, being out at this time of the morning, so you decide to ignore it. But the voice comes again, "Good morning". Finally you locate the other nut who has gotten up at this hour, far across the lake -- much further than you could normally hear a voice. That fisherman is aware of the early morning lake's effect on sound transmission. The cool water keeps the air near the water cool, but the early sun has begun to heat the air higher up, creating a "thermal inversion". The fact that the speed of sound is faster in warmer air bends some sound back downward toward you - sound that would not reach your ear under normal circumstances. This natural amplification over cool bodies of water is one of the few natural examples of sound refraction.
Interference of Sound
Interference of Sound
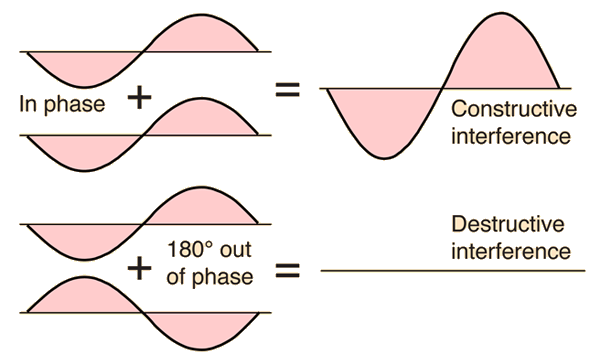
Two traveling waves which exist in the same medium will interfere with each other. If their amplitudes add, the interference is said to be constructive interference , and destructive interference
if they are "out of phase" and subtract. Patterns of destructive and constructive interference may lead to "dead spots" and "live spots" in auditorium acoustics. Interference of incident and reflected waves is essential to the production of resonant standing waves.
Interference has far reaching consequences in sound because of the production of "beats" between two frequencies which interfere with each other.
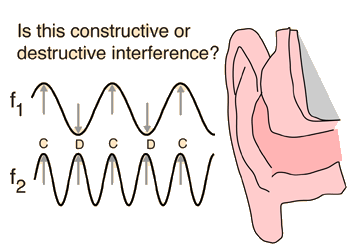
Visualization of phase
Interference with a Tuning Fork
 If you strike a
If you strike a
tuning fork and rotate it next to your ear, you will note that the sound alternates between loud and soft as you rotate through the angles where the interference is constructive and destructive.
Each tine of the fork produces a pressure wave which travels outward at the speed of sound. One part of the wave has a pressure higher than atmospheric pressure, another lower. At some angles the high pressure areas of the two waves coincide and you hear a louder sound. At other angles, the high pressure part of one wave coincides with the low pressure part of the other.
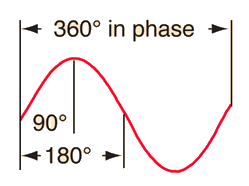
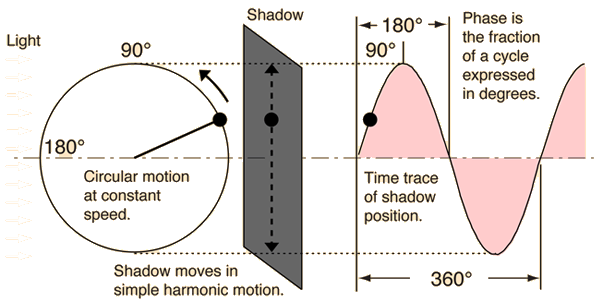
Phase
If a mass on a rod is rotated at constant speed and the resulting circular path illuminated from the edge, its shadow will trace out simple harmonic motion
. If the shadow vertical position is traced as a function of time, it will trace out a sine wave. A full period of the sine wave will correspond to a complete circle or 360 degrees. The idea of phase follows this parallel, with any fraction of a period related to the corresponding fraction of a circle in degrees.
Interference and Phase
Reflection of Sound
Reflection of Sound
The reflection of sound follows the law "angle of incidence equals angle of reflection", sometimes called the law of reflection
. The same behavior is observed with light and other waves, and by the bounce of a billiard ball off the bank of a table. The reflected waves can interfere with incident waves, producing patterns of constructive and destructive interference. This can lead to resonances called standing waves
in rooms. It also means that the sound intensity near a hard surface is enhanced because the reflected wave adds to the incident wave, giving a pressure amplitude that is twice as great in a thin "pressure zone
" near the surface. This is used in pressure zone microphones to increase sensitivity. The doubling of pressure gives a 6 decibel increase in the signal picked up by the microphone. Reflection of waves in strings
and air columns
are essential to the production of resonant standing waves in those systems.

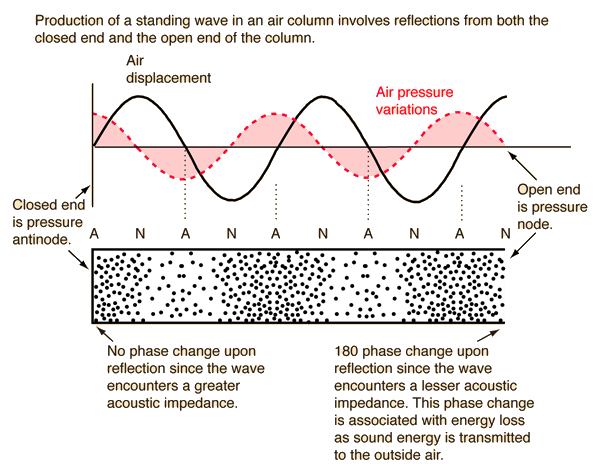
Phase Change Upon Reflection
The phase of the reflected
sound waves from hard surfaces and the reflection of string waves from their ends determines whether the interference of the reflected and incident waves will be constructive or destructive. For string waves at the ends of strings there is a reversal of phase
and it plays an important role in producing resonance
in strings
. Since the reflected wave and the incident wave add to each other while moving in opposite directions, the appearance of propagation is lost and the resulting vibration is called a standing wave
.
When sound waves in air (pressure waves) encounter a hard surface, there is no phase change upon reflection. That is, when the high pressure part of a sound wave hits the wall, it will be reflected as a high pressure, not a reversed phase which would be a low pressure. Keep in mind that when we talk about the pressure associated with a sound wave, a positive or "high" pressure is one that is above the ambient atmospheric pressure and a negative or "low" pressure is just one that is below atmospheric pressure. A wall is described as having a higher "acoustic impedance" than the air, and when a wave encounters a medium of higher acoustic impedance there is no phase change upon reflection.
On the other hand, if a sound wave in a solid strikes an air boundary, the pressure wave which reflects back into the solid from the air boundary will experience a phase reversal - a high-pressure part reflecting as a low-pressure region. That is, reflections off a lower impedance medium will be reversed in phase.
Besides manifesting itself in the "pressure zone
" in air near a hard surface, the nature of the reflections contribute to standing waves in rooms and in the air columns which make up musical instruments.
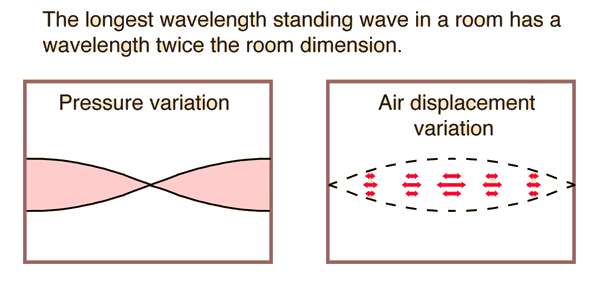
Pressure Zone
The sound intensity
near a hard surface is enhanced because the reflected wave adds to the incident wave, giving a pressure amplitude that is twice as great in a thin "pressure zone" near the surface. This is used in pressure zone microphones
to increase sensitivity. The doubling of pressure gives a 6 decibel
increase in the signal picked up by the microphone.
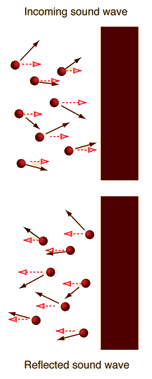
This is an attempt to visualize the phenomenon of the pressure zone in terms of the dynamics of the air molecules involved in transporting the sound energy. The air molecules are of course in ceaseless motion just from thermal energy
and have energy as a result of the atmospheric pressure
. The energy involved in sound transport is generally very tiny compared to that overall energy. If you visualize the velocity vectors shown in the illustration as just that additional energy which associated with the sound energy in the longitudinal wave
, then we can argue that the horizontal components of the velocities will just be reversed upon collision with the wall. Presuming the collisions with the wall to be elastic
, no energy is lost in the collisions.
Viewing the collection of molecules as a "fluid", we can invoke the idea that the internal pressure of a fluid is a measure of energy density
. The energy of the molecules reflecting off the wall adds to that of the molecules approaching the wall in the volume very close to the wall, effectively doubling the energy density and hence the pressure associated with the sound wave.
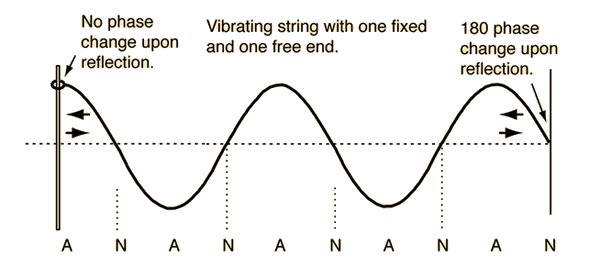
The conditions which lead to a phase change on one end but not the other can also be envisioned with a string if one presumes that the loose end of a string is constrained to move only transverse to the string. The loose end would represent an interface with a smaller effective impedance and would produce no phase change for the transverse wave. In many ways, the string and the air column are just the inverse of each other.
ใกล้พื้นผิวนี้ ใช้ในไมโครโฟน เพื่อเพิ่มความดังของเสียงที่เพิ่มขึ้น สามารถเพิ่มความแรงของสัญญาณเพิ่มขึ้น 6 เดซิเบล จากการสะท้อนคลื่น
ในห้อง นอกจากนี้ยังหมายถึง ความเข้มของเสียงใกล้พื้นผิวแข็งจะเพิ่มขึ้นเนื่องจากคลื่นสะท้อนจะเพิ่มความเข้มของคลื่น แรงกด ของ Amplitude มีแรงกดสูงกว่าสองเท่าใน "pressure zone "
คุณสมบัติเช่นเดียวกันนี้เกิดขึ้นกับคลื่นแสงและคลื่นอื่น ๆ เช่นเดียวกับการเด้งลูกบิลเลียดออกจากมุมสะท้อนของโต๊ะ คลื่นที่สะท้อนสามารถรบกวนคลื่นที่เกิดขึ้นสร้างรูปแบบของการแทรกแซงที่เป็นรูปธรรมและการทำลายล้าง สามารถนำไปสู่ resonances เรียกว่าคลื่นนิ่ง
การสะท้อนของเสียงเป็นไปตามกฎ "มุมตกเท่ากับมุมสะท้อน" บางครั้งเรียกว่ากฎของการสะท้อน
การสะท้อนเสียง
อนุกรมหางเสียง
Harmonic series
Harmonics and Overtone
เครื่องดนตรีอิเล็กทรอนิกส์บางชนิด เช่น Synthesizer สามารถเล่นคลื่นความถี่บริสุทธิ์ได้โดยไม่มีการ overtones (คลื่นซายน์)Synthesizer ยังสามารถผสมความถี่บริสุทธิ์ เข้าด้วยกันให้เป็นโทนเสียงที่ซับซ้อนมากขึ้น เป็นการจำลองเสียงให้เหมือนกับเครื่องดนตรีอื่น ๆ Flute แล Ocarinas บางอย่างมีเสียงใกล้เคียงกัน โดยไม่มี Overtone
Overtone เป็นส่วนหนึ่งของ Partial ที่อยู่ด้านบนของเสียงที่ต่ำสุด คำว่า overtone ไม่ได้หมายความถึง Harmonicity หรือ inharmonicity และไม่มีความหมายพิเศษอื่นนอกเหนือจาก เสียงพื้นฐาน ทั้งหมดเป็นความสัมพันธ์ ของความแตกต่าง ของเสียงที่เกิดจากเครื่องดนตรี โดยเฉพาะด้านสีสัน (timbre, Tone color, หรือลักษณะของเสียง) เมื่ออธิบายถึงคำว่า Overtone หรือ ตัวเลขของ Partial ต้องระวังเรื่องความแตกต่างที่ทำให้เกิดความสับสนได้ เช่น โอเวอร์โทนที่สอง อาจจะไม่ใช่ Third Partial เพราะมันหมายถึง เสียงลำดับที่สอง ใน Series
The second harmonic, whose frequency is twice of the fundamental, sounds an octave higher; the third harmonic, three times the frequency of the fundamental, sounds a perfect fifth above the second harmonic. The fourth harmonic vibrates at four times the frequency of the fundamental and sounds a perfect fourth above the third harmonic (two octaves above the fundamental). Double the harmonic number means double the frequency (which sounds an octave higher).
The harmonic series is an arithmetic series (1×f, 2×f, 3×f, 4×f, 5×f, ...). In terms of frequency (measured in cycles per second, or hertz (Hz) where f is the fundamental frequency), the difference between consecutive harmonics is therefore constant and equal to the fundamental. But because human ears respond to sound nonlinearly, higher harmonics are perceived as "closer together" than lower ones. On the other hand, the octave series is a geometric progression (2×f, 4×f, 8×f, 16×f, ...), and people hear these distances as "the same" in the sense of musical interval. In terms of what one hears, each octave in the harmonic series is divided into increasingly "smaller" and more numerous intervals.


Frequencies, wavelengths, and musical intervals
Musical Interval
Wavelengths
wavelengths
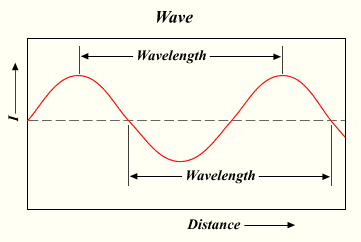
ความยาวคลื่น คือระยะทางระหว่างส่วนที่ซ้ำกันของคลื่น
สัญลักษณ์แทนความยาวคลื่นที่ใช้กันทั่วไปคือ อักษรกรีก
แลมบ์ดา (λ).
แกนนอนในแผนภูมิแทนระยะทาง และแกนตั้งแทนค่า ณ เวลาหนึ่ง ของปริมาณหนึ่งซึ่งกำลังเปลี่ยนแปลง (ตัวอย่างเช่น สำหรับคลื่นเสียง ปริมาณที่กำลังเปลี่ยนแปลงก็คือแรงดันอากาศ หรือสำหรับคลื่นแม่เหล็กไฟฟ้า ปริมาณที่กำลังเปลี่ยนแปลงก็คือสนามไฟฟ้าและสนามแม่เหล็ก) ซึ่งเป็นฟังก์ชันของระยะทาง
ความยาวคลื่น λ สัมพันธ์แบบผกผันกับความถี่
ของคลื่นนั้น โดยความยาวคลื่นมีค่าเท่ากับความเร็วของคลื่นนั้นๆ หารด้วยความถี่ ถ้าเราพิจารณาคลื่นแม่เหล็กไฟฟ้าในสุญญากาศ ความเร็วนั้นก็คือความเร็วแสงนั่นเอง ความสัมพันธ์นี้สามารถเขียนได้เป็น

เมื่อ: λ = ความยาวคลื่น
c = ความเร็วของคลื่น
f = ความถี่ของคลื่น
เมื่อแทนค่าการหาความยาวคลื่นของความถี่ใด ๆ ต้องมีการคำนึงถึงอุณหภูมิด้วยเสมอโดยเฉพาะความถี่ของคลื่นเสียง เช่น การหาความยาวคลื่นของความถี่ 40 Hz ที่อุณหภูมิ 25 องศาเซลเซียส มีการหาดังนี้
λ = 331.4 + ((0.6) X 25)
40 Hz
ได้ความยาวคลื่น = 8.66 เมตร
Frequencies
frequencies

Terminology
Partial, harmonic, fundamental, inharmonicity, and overtone[edit]
A "complex tone" (the sound of a note with a timbre particular to the instrument playing the note) "can be described as a combination of many simple periodic waves (i.e., sine waves) or partials, each with its own frequency of vibration, amplitude, and phase."[4] (See also, Fourier analysis.)
A partial is any of the sine waves (or "simple tones", as Ellis calls them when translating Helmholtz) of which a complex tone is composed, not necessarily with an integer multiple of the lowest harmonic.
A harmonic is any member of the harmonic series, an ideal set of frequencies that are positive integer multiples of a common fundamental frequency. The fundamental is obviously a harmonic because it is 1 times itself. A harmonic partial is any real partial component of a complex tone that matches (or nearly matches) an ideal harmonic.[5]
An inharmonic partial is any partial that does not match an ideal harmonic. Inharmonicity is a measure of the deviation of a partial from the closest ideal harmonic, typically measured in cents for each partial.[6]
Many pitched acoustic instruments are designed to have partials that are close to being whole-number ratios with very low inharmonicity; therefore, in music theory, and in instrument design, it is convenient, although not strictly accurate, to speak of the partials in those instruments' sounds as "harmonics", even though they may have some degree of inharmonicity. The piano, one of the most important instruments of western tradition, contains a certain degree of inharmonicity among the frequencies generated by each string. Other pitched instruments, especially certain percussion instruments, such as marimba, vibraphone, tubular bells, timpani, and singing bowls contain mostly inharmonic partials, yet may give the ear a good sense of pitch because of a few strong partials that resemble harmonics. Unpitched, or indefinite-pitched instruments, such as cymbals, gongs, or tam-tams make sounds (produce spectra) that are rich in inharmonic partials and may give no impression of implying any particular pitch.





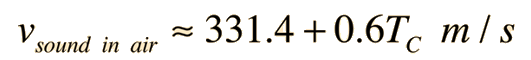


 One consequence of
One consequence of 
 Sound propagates in all directions from a point source. Normally, only that which is initially directed toward the listener can be heard, but refraction can bend sound downward. Normally, only the direct sound is received. But refraction can add some additional sound, effectively amplifying the sound. Natural amplifiers can occur over cool lakes.
Sound propagates in all directions from a point source. Normally, only that which is initially directed toward the listener can be heard, but refraction can bend sound downward. Normally, only the direct sound is received. But refraction can add some additional sound, effectively amplifying the sound. Natural amplifiers can occur over cool lakes.


 If you strike a
If you strike a














