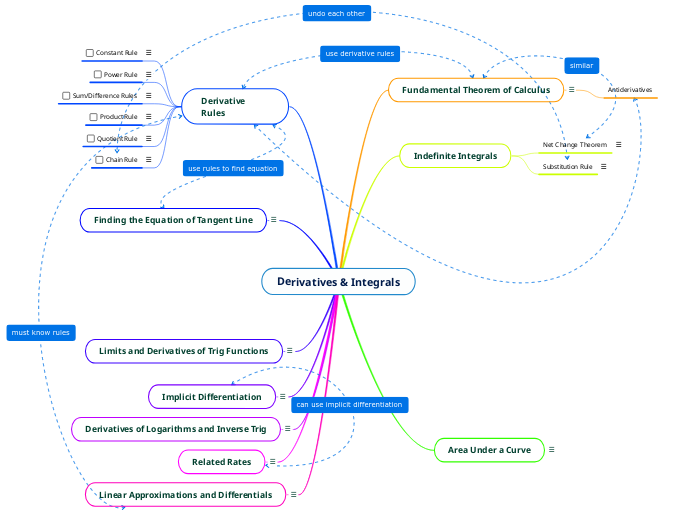
Derivatives & Integrals

Mere som dette

Plural y Singular

af Jose corella

Principles of Calculus

af Kaushik Krishna

Track and Field

af felicia situil

Circles

af NABIHA AKHTER

Linear Approximations and Differentials

The Linear Approximation to f at a is the linear function:

$L(x)=f(a)+f'(a)(x-a)$

Related Rates

Related rates are referring to the numbers or measurements that are being compared by way of a ratio. We are concerned with a special ratio in which the two terms that are being compared are in two different units of measure.

For example, $dA/dr$ is referring to the change in area with respect to the change in radius. How fast is the area changing when the radius changes?

When doing related rate problems it will be helpful to know some general math equations such as the equation for the area of circle, volume of a cube, and the equation for the area of a triangle, etc.

Derivatives of Logarithms and Inverse Trig

Natural Log:

$d/dx(lnx)=1/x$

Ex.

$d/dx(ln(5x))$

$d/dx(ln5+lnx)$

$=0+1/x$

Inverse Trig Functions:

Remembering you trig identities such as SOHCAHTOA and the Pythagorean Identities will help you manipulate equations when you need to find the derivative.

if $y=sin^-1x$ (sin should be raised to -1) then $x=siny$

Derivative of Logs

$d/dx(logbx)=1/xlnb$

Implicit Differentiation

Implicit Equations are equations that are not written in terms of only one variable.

The notation $dy/dx$ means you take the derivative of y with respect to x.

Limits and Derivatives of Trig Functions

$d/dx(sinx)=limh-0((sin(x+h)-sinx)/h$

derivative of sin(x) is equal to the limit of sin(x+h) minus sin(x) all over h as h goes to zero.

It is helpful to know your trig identities when taking the derivative of trig functions that way you can better manipulate the equation.

$d/dx(sinx)=cosx$

$d/dx(cosx)=-sinx$

$d/dx(tanx)=sec^2x$

$d/dx(cotx)=-csc^2x$

$d/dx(secx)=secxtanx$

$d/dx(cscx)=-cscxcotx$

Finding the Equation of Tangent Line

To find the equation of a tangent line to a given function at a given point we use $y-f(x1)=f'(x1)(x-x1)$ . In order to use this form we need to find the output or the y value of the original function at the given point and the derivative of the given function and plug the given x value in. Then take these values and plug into the given form and simplify.

Derivative Rules

Chain Rule

Function within a function

The derivative of the inside times the derivative of the outside.

Ex.

$f(x)=sin^4(x)$

$=(sin(x))^4$

we set "u" equal to sin x and f(u) equal to u raised to the 4th power, then find the derivative of both and multiple together substituting sin x into the derivative of f(u).

$f'(x)=4cosxsin^2x$

Quotient Rule

$W(x)/Z(x)=(W'(x)*Z(x)-W(x)*Z'(x))/Z(x)^2$

The derivative of the top times the bottom minus the derivative of the bottom times the top all over the bottom squared.

Product Rule

$(W*Z)=W'*Z+W*Z'$

The derivative of the first times the second plus the derivative of the second times the first.

Sum/Difference Rules

$d/dx(f+ or -g)=d/dx(f)+ or - d/dx(g)$

Power Rule

$f(x)=x^n$

$d/dx(x^n)=nx^(n-1)$

should be nx to the power of n-1.

Ex.

$f(x)=x^9$

$d/dx(x^9)=9x^8$

Constant Rule

The derivative on a constant is just zero.

Ex.

$d/dx(5)=0$

Area Under a Curve

There are 3 different ways to choose the values for x1,x2,x3 etc.

Left endpoint of each subinterval
Right endpoint of each subinterval
Midpoint of each subinterval

The change in x is equal to $(b-a)/n$

For the left endpoint method we do f(0) times the change of x and we do this for all 4 quadrants. We start with 0 since its left endpoint method.
For the right endpoint method we do f(1) times the change of x and we do this for all 4 quadrants. We started with 1 since its right endpoint method.
For midpoint method you take the middle of each quadrant and multiple each on by the change of x.

Indefinite Integrals

Substitution Rule

If $u=g(x)$ is a differentiable function whose range is an interval I and f is continuous on I, then the integral of $f(g(x))*g'(x)dx$ is equal to the integral of $f(u)du$

Ex.

Find the integral of $4xsin(x^4)dx$

First set $u=x^4$ and $f(u)=sinu$

Then say $du=2xdx$ and get dx alone $du/2x=dx$

Next step would be to go back to the original integral and

substitute u for $x^4$ and $du/4x$ for $dx$ the 4x at the front

and the 4x in the denominator will cancel leaving you with

the integral of $sin(u)du$ which will be $-cos(u)+C$ then

we will substitute our 'u' which was $x^4$ for the 'u' which

will give us $-cos(x^4)+C$

Link:

Substitution Rule and Chain Rule undo each other.

Net Change Theorem

The integral of the rate of change is the net change.

The integral of $F'(x)dx$ from a to b is equal to $F(b)-F(a)$

Fundamental Theorem of Calculus

The area function with constant endpoint 'a' is

$A(x)$ equals the integral of $f(t)dt$ from a to x. where you take the given 'x' and make that the endpoint, where x is greater than or equal to a. This gives us the net area of the region bounded by the graph of f and the t-axis on the interval [a,x]

$g(x)$ is equal to the integral of $f(t)dt$ from a to x. and $g'(x)=f(x)$

The integral of $f(x)dx$ from a to b is equal to $F(b)-F(a)$

where F is any antiderivative of f, a function in which $F'=f$