af Mariluz Achiri Ccahua 7 år siden
388
diseño 2
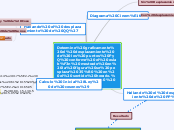
Se examina el desplazamiento de los puntos P y Q cuando el eslabón del mecanismo se mueve 35 grados en sentido horario. Se utilizan diferentes leyes trigonométricas, como la ley de cosenos y la ley de senos, para calcular las nuevas posiciones de estos puntos.