Elementary Mathematics Week 12-13
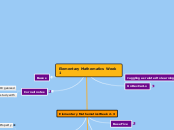
Exponent Rules
Raising a power to a power
When you raise a power to a power, you multiply the exponents
Multiply/Divide same base, diff. exponents
Add/Subtract (respectively) exponents together, keep the base
Fraction Memorization
1/2 = 0.50
1/3 = 0.33...
2/3 = 0.66...
1/4 = 0.25
3/4 = 0.75
1/5 = 0.20
2/5 = 0.40
3/5 = 0.60
4/5 = 0.80
1/10 = 0.10
3/10 = 0.30
7/10 = 0.70
9/10 = 0.90
Proper Terminology
a. 3(-4) = Three groups of four negatives
b. -3(4) = Take away three groups of four positives
c. -3(-4) = Take away three groups of four negatives
d. 3(1/2) = Three groups of half a positive
e. 3(-1/2) = Three groups of half a negative
f. 10 / 2 = Ten divide into how many groups of two?
g. 10 / (1/2) = Ten divided into how many groups of one-half
h. 1/2 / (1/3) = One-half is equal to how many groups of one-third?
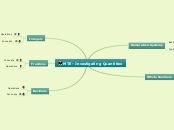
Elementary Mathematic Week 10-11
Fractions in Equations
*Multiply by what is missing*
- Break up the denominator if possible to see exactly what is missing
- Multiply in fractions (i.e. instead of multiplying 5, multiply by 5/5)
Subtracting Fractions
-Find common denominator by multiplying what is missing
-Subtract the numerators and keep the denominator
-Simplify
Adding Fractions
-Find common denominator by multiplying by what is missing
-Add the numerators and leave the denominator the same
-Simplify
Benchmarks
Benchmark numbers are those that are easier to round to or know for reference. Start with 1 and 1/2 and once the students get better with those, introduce 1/4 and 3/4.
Demonstrating Fractions
Every person learns differently and what works for one person may not work for another. My personal favorite is the fraction tiles but I know that some people probably hate them.
Variosu Polygons
Pie Fractions
Blocks
Two Colored Tiles
Fraction Tiles
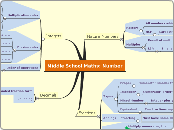
Elementary Mathematics Week 8-9
Multiplying Binomials and other Polynomials
Area Model
The area model is great because it can be used with any two polynomials. Also refered to as the magic square! Check hyperlink for example. Think floors and rooms.
Multiplying Integers
This method is similar to the "adding integers".
2(6)= Two groups of six positives
3(-5)= Three groups of five negatives
-3(6)= Take away three groups of six positives
-2(-4)= Take away two groups of four negatives
*Zero banks must be used in the last two examples*
Elementary Mathematics Week 6-7
GCF (Greatest Common Factor)
Number Tiles
Tiles are great for students learning this so that they see the physical representation of the numbers. Ask which tile is the "longest" and present in both.
Prime Factorization
Numbers are divided by prime numbers until they become a prime number. The like terms are pulled and the product is the GCF
12: 1, 2, 3, 4, 6, 12
18: 1, 2, 3, 6, 9, 18
The GFC here is 6
Adding Integers
Missing Addend
5 + 2 = x
becomes
5 = x - 2
The students should be very familiar and comfortable with fact families to succeed with this method
Number Line Addition
-2 + 5
A # line is draw. A dot is draw at the first number (-2) and "hop" lines are draw according to the second number (moving to the right 5)
Modeling Integers
-1 + 5
+++++
_
The neg. 1 is represented by the red minus sign and the pos. 5 is represented by the blue plus signs.
LCM (Least Common Multiple)
Prime Factoization
Each number is divided by a prime number until all that is left is a prime number. The numbers are then multiplied (the greatest exponent of each number). The product is the LCM
Listing
12: 12, 24, 36, 48, 60
18: 18, 36, 54
The LCM is 36
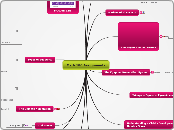
Elementary Mathematics Week 4-5
Estimation
Clustering
Rounding
Grouping
Front-End
Mental Math (Add.)
Breaking Up
Adding From the Left
Compatible Numbers
Trading Off (Balancing)
Mental Math (Sub.)
Breking Up
Drop the Zeros
Trading Off
Divisibility Rules
Elementary Mathematics Week 2-3
Addition Properties
a + b = b + a
a + (b + c) = (a + b) + c
a + 0 = a = 0 + a
Multiplication Properties
Commutative Property
a*b = b*a
Associative Property
a*(b*c) = (a*b)*c
Closure Property
Identity Property
a*1 = a = 1*a
Base Five
Any number in base 10 can be changed to base 5 by dividing the original number by 5 until it can no longer continue. The remander of each time should be recorded along the side.
Elementary Mathematics Week 1
Cornell notes
The cornell notes shown in the attched website are not exactly the same as the ones we did in class but they are very similar. The only difference is that the equation is written on both sides of the dividing line; this makes it very useful for studying directly from the notes.
Easy to study with
Organized
Bases
UnDevCarLo
1. Understand the Problem
2. Develop a Plan
3. Carry out the Plan
4. Look Back
Juggling as related to learning
I very much enjoyed how the class was told to juggle after watching Mr. Miltenberger juggle for the majority of the class. I appreciate it because it made the class realize that we did not learn by watching him, instead, we learned by doing. It was a valuable lesson.