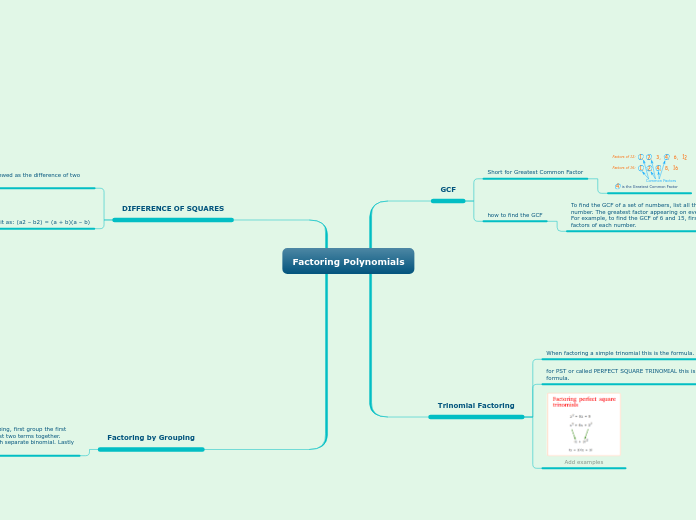
Factoring Polynomials
A noun is a word that functions as the name of some specific thing or set of things, such as living creatures, objects, places, actions, qualities, states of existence, or ideas.
Factoring by Grouping
A concrete noun is a noun that can be identified through one of the five senses (taste, touch, sight, hearing, smell).
we can factor a polynomial by grouping, first group the first two terms together, and then the last two terms together. secondly, factor out a GCF from each separate binomial. Lastly factor out the common binomial.
Subtopic
DIFFERENCE OF SQUARES
Possessive nouns are nouns which possess something, normally another noun.
We can factor it as: (a2 – b2) = (a + b)(a – b)
When an expression can be viewed as the difference of two perfect squares.
Trinomial Factoring
A noun which cannot be identified by using one of the five senses (taste, touch, sight, hearing, smell).
Add examples
for PST or called PERFECT SQUARE TRINOMIAL this is the formula.
(a2 + 2ab + b2) = (a + b)2
(a2 - 2ab + b2) = (a - b)2
When factoring a simple trinomial this is the formula.
(ax2 + bx + c)
GCF
Irregular nouns are nouns which don’t follow a spelling pattern when pluralized.
how to find the GCF
To find the GCF of a set of numbers, list all the factors of each number. The greatest factor appearing on every list is the GCF. For example, to find the GCF of 6 and 15, first list all the factors of each number.
Short for Greatest Common Factor