af Ariana Perez 5 år siden
2178
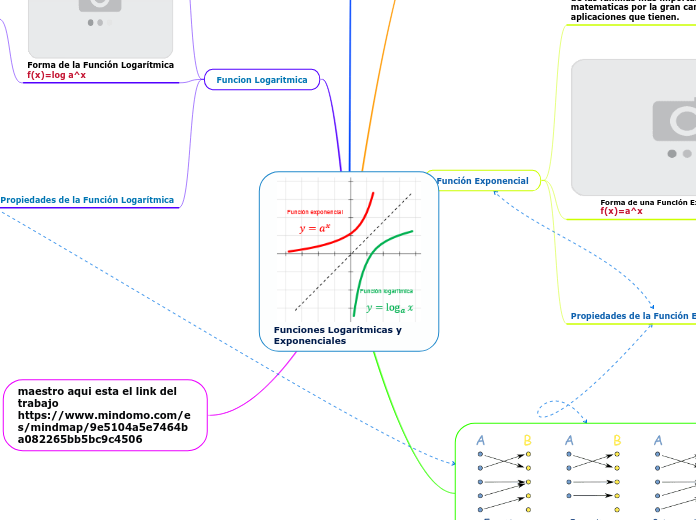
Funciones Logarítmicas y Exponenciales
Logaritmiske og eksponentielle funksjonar spelar ei viktig rolle i matematikk, særleg på grunn av deira omfattande bruksområde. Ei logaritmisk funksjon kan uttrykkast som f(x) = log_