integral
Técnicas de Integração
Integração por Substituição
é um método para resolver integral
inspirada na Regra da Cadeia para derivadas
(f.g)'(x)=f'(g(x)).g'(x)
a integral de um produto de funções
não é o produto das integrais
Teorema Fundamental
do Cálculo
torna possível o cálculo de Integrais
Definidas, e de variações acumuladas,
de um modo alternativo ao cálculo das
Somas de Riemann.
busca uma função primitiva
integral indefinida
e igual F(t)+c
Teorema Fundamental
do Cálculo parte 2
com uma integral definida de (a,x)em
que a função y = f(t) é positiva, e o
valor x satisfaz x>a
Teorema do Confronto nos permite
afirma que dA/dx=f(x)
Integral Indefinida de somas
e produto por constante.
Integral Indefinida do produto de
uma função por constante
A derivada do produto de uma função
por uma constante é igual à constante
multiplicada pela derivada da função
Integral Indefinida de uma soma de funções
a Integral Indefinida da soma de funções é
a soma das Integrais Indefinidas.
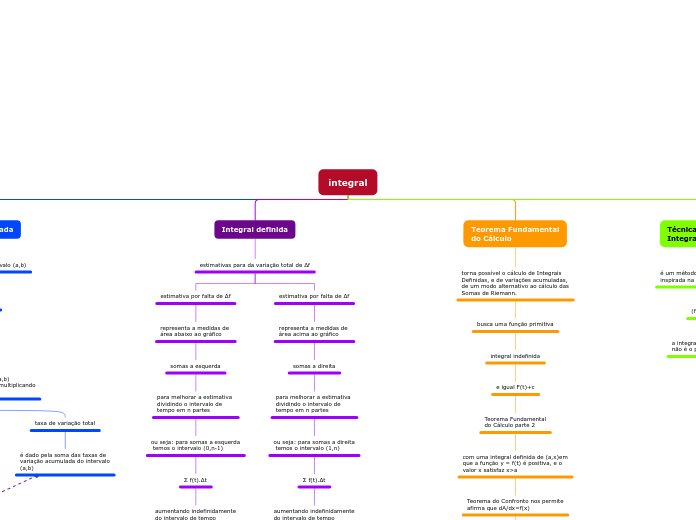
Integral definida
estimativas para da variação total de Δf
representa a medidas de
área acima ao gráfico
somas a direita
ou seja: para somas a direita
temos o intervalo (1,n)
aumentando indefinidamente
do intervalo de tempo
ou seja: calculamos o limite
da soma a direita com
n tendendo ao infinito
estimativa por falta de Δf
representa a medidas de
área abaixo ao gráfico
somas a esquerda
para melhorar a estimativa
dividindo o intervalo de
tempo em n partes
ou seja: para somas a esquerda
temos o intervalo (0,n-1)
Σ f(t).Δt
aumentando indefinidamente
do intervalo de tempo
ou seja: calculamos o limite
da soma a esquerda com
n tendendo ao infinito
definição de área
sob uma curva
para uma função positiva em (a,b)
o valor da Integral Definida
representa a medida da área abaixo
da curva do gráfico da função acima
do eixo x, e entre as retas x = a e
x = b.
Soma algébrica de área
O valor da integral definida representa
uma soma de áreas entre a curva do
gráfico da função e o eixo x, em que
as áreas acima do eixo são computadas
positivamente, e as áreas abaixo do
eixo são computadas negativamente
Variação acumulada
variação acumulada no intervalo (a,b)
taxa de variação
instantânea
y=dF/dt=f(t)
ou
y=ΔF/Δt=f(t)
sabendo f(t) e Δt no intervalo (a,b)
podemos estimar o valor de Δf multiplicando
f(t) por Δt ou seja: f(t).Δt=Δf
taxa de variação total
é dado pela soma das taxas de
variação acumulada do intervalo
(a,b)
taxa de variação acumulada
é o valor de Δf calculado em pequenos
intervalos de tempo de (a,b).
variação acumulada
por falta e por excesso
variação acumulada
por excesso
consideramos os últimos valores
obtidos no intervalo (a,b)
ou seja no intervalo (a+1,b)
obtendo então uma estimativa
maior que o valor real de Δf
ou seja: estimativa por excesso > Δf
variação acumulada
por falta
consideramos os primeiros valores
obtidos no intervalo (a,b)
ou seja no intervalo (a,b-1)
obtendo então uma estimativa
menor que o valor real de Δf
ou seja: estimativa por falta < Δf