LOS NÚMEROS
NÚMEROS RACIonales
Los números racionales contienen a los números enteros, por lo tanto, contienen a los números naturales.
Puede ser impulsado en fracciones o con decimales.
el conjunto de todos los números racionales se indican como Q siendo esta letra la inicial de la palabra francesa "Quotient".
Un números racional es de forma a/b, siendo (a) el numerador y (b) el denominador de la fraccion.
Los números racionales se pueden representar como el cociente de dos números enteros o, más exactamente, un número entero y un positivo natural
Cada numero racional se puede representar con infinitas fracciones equivalentes
el conjunto de los números enteros esta contenido en el conjunto de los números racionales, que matemáticamente se escriben
3/8=0.375
2/5=0.4
NÚMEROS ENTEROS
Los números enteros, se representa medianamente la letra Z, que proviene de la inicial de la palabra alemana Zhal que significa "numero",
Z={...-4,-3-2,-1,0,1,2,3,4,...}
los números entero es un numero natural con signo mas (+) o menos (-)
división
15/3=5
la división es la operación inversa de la multiplicación, donde m=n*p, entonces la división es P=m/n
multiplicación
(-5)*(-3)=5*3=15
5*3=15
dos números enteros, se multiplican (m) según la siguiente regla m=n*p
RestA
Por ejemplo
-10+9=-1
9-10=-1
En el conjunto Z, las restas pueden realizarse independientemente del orden de los números
Por ejemplo 5+2= 2+5
propiedades de la suma de enteros ley de composición interna
Elemento neutro
Tienen un orden, los números positivos son mayores que cero (0) (el número positivo menor es 1), los números negativos son menores que cero (0) (el número negativo mayor es -1).
La cantidad de números enteros que existen son infinita.
An el conjunto Z, las restas pueden realizarse independientemente del order de los numeros
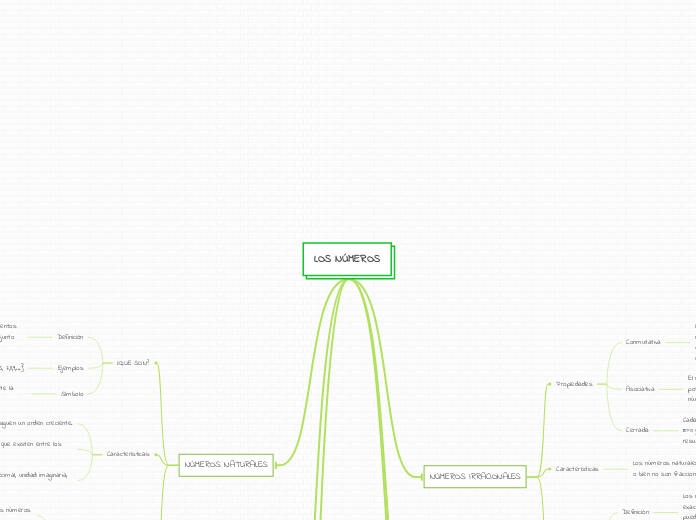
NÚMEROS NATURALES
sum
En una recta señalamos un punto, que marcamos con el número cero. A la derecha del cero, y con las mismas separaciones, situamos de menor a mayor los números naturales: 1, 2, 3...
Los números naturales se pueden representar en una recta ordenados menor a mayor
La operación matemática que resulta al reunir dos números o más para obtener una cantididad final.
La cantidad de números naturales que existen entre los números naturales es infinita.
Los números naturales siguen un orden creciente.
Los números naturales, se representa medianamente la letra N, por tanto, N={0,1,2,3,4,...}
N={0,1,2,3,4,5,6, 7,8,9,...}
los números naturales se usan para contar los elementos de un conjunto, todos estos números forman un conjunto llamado "Conjunto de Números Naturales"
Your text here
NÚMEROS REALES
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales.
NÚMEROS IRRACIONALES
¿QUE SON?
Símbolo
Los numeros irracionales, se representan medianamente el numero pi I
Ejemplos
Número Áureo φ = 1.61803398874989…
π=3.1415926535897932384…
√2, √3, √5, √7 ...
Definición
Los números irracionales no pueden expresarse exactamente en forma de fracción común o decimal, aunque pueden clacularse con los decimales que se deseen (no son decimales periódicos ni semiperiodos).
Características
Los números naturales no tienen decimal, unidad imaginaria, o bien no son fracciones.
Propiedades
Cerrada
Cada número tiene su negativo que lo anula, por ejemplo π-π=0 y de la misma un inverso multiplicativo que da como resultado 1, es decir ϕ× 1/ϕ=1.
Asociativa
El resultado de la suma, resta, multiplicación, división o potenciación de un número irracional, siempre será un número irracional.
Conmutativa
La distribución y agrupación de los números da como resultado el mismo número, independientemente de su agrupación, siendo (ϕ+π)+e=ϕ+ (π+e); y de la misma manera con la multiplicación, (ϕ×π) ×e=ϕ× (π×e).