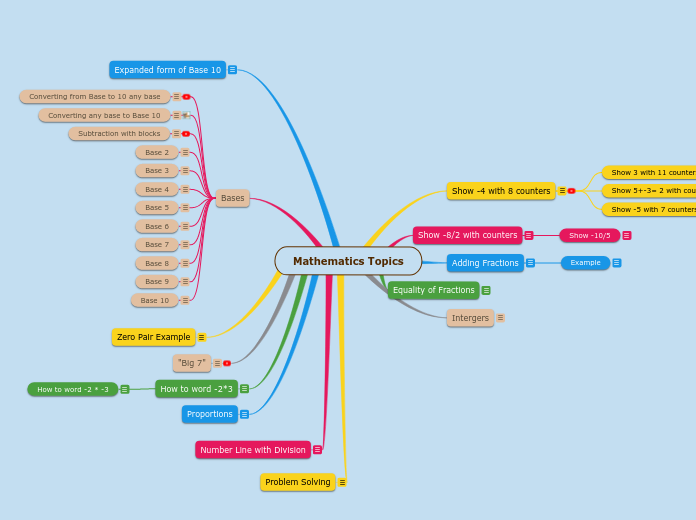
Mathematics Topics
Problem Solving
Problem Solving in math is when you look at a problem and determine the best way to start the problem is. Then you solve the problem and double check your answer. When you double check your answer, and you get the same thing you started with, that's how you know you got it correct.
Number Line with Division
Number line with division
12/4
0 1 2 3 4 5 6 7 8 9 10 11 12
We start at 12 and take 4 steps towards 0. That puts us at 8. Then takes another 4 steps. That puts us at 4. Take another 4 steps. That puts us at 0.
So 12/4 = 3
Proportions
A proportions is a statement that says that two ratios are equal.
Example
1/3 = 2/6
How to word -2*3
-2 *3
This means that you have -( 2*3).
So you start with 2 groups of positive 3
+++ +++
You need to take the opposite of the groups, so that makes the positive negative
--- ---
The final answer would be -6
The opposite of 2 groups of 3
How to word -2 * -3
How to word -2 * -3
You start with 2 groups of negative 3
--- ---
But you need to take the opposite of the negative, which makes it positive.
+++ +++
So -2*-3 = 6
The opposite of 2 groups of -3
Intergers
An integer is a whole number (not a fraction)
1,2,3,4,...
Equality of Fractions
Example
(12/42) and (10/35)
Find the LCM
the factors are 2*3*5*7=210
(12/42) turns into 60/210
(10/35) turns into 60/210
these fractions are equal
Adding Fractions
Adding Fractions
Example
(-2/3) + (1/5)
Find common denominator
(-2/3) turns into (-10/15)
(1/5) turns into (3/15)
(-10/15) + (3/15) = -7/15
Just add straight across. Don't change the denominator.
Example
Example #2
(1/2) + (1/6)
(1/2) turns into (3/6)
(1/6) stays (1/6)
(3/6) + (1/6) = (4/6) = (2/3)
Show -8/2 with counters
-8/2
Switch the division to multiplication
2* ? = -8
? = -4
So you must have 2 groups of negative 4
---- ----
Show -10/5
Show -10/5
Switch it to multiplication
5* ? = -10
? = -2
So you have 5 groups of negative 2
-- -- -- -- --
Show -4 with 8 counters
To show -4 with 8 counters, you would use 6 negative counters and 2 positive counters
- - - - - -
++
This cancels out 2 pairs, and leaves 4 negatives.
-6+2=-4
Show -5 with 7 counters
Show -5 with 7 counters
- - - - - -
+
-6 + 1 = -5
One pair cancels out leaving -5
Show 5+-3= 2 with counters
Show 5+-3=2 with counters
+++++
- - -
Three pairs are cancelled out and 2 is left over
Show 3 with 11 counters
To show 3 with 11 counters you would need 7 positive counters and 4 negative counters
+++++++
----
This cancels out 4 pairs and leave 3 positive counters
7 + (-4) = 3
"Big 7"
The Big 7
This is an easier way for students to divide numbers.
Example:
137/3
Students like to work with the number 10. So if we use 10's while dividing, it is easier for them.
Create the division problem like a normal long division problem. The first step is to multiply 10 *3 to get 30. We then subtract the 30 from the 137 to get 107. We then multiply 10*3 = 30 and subtract the 30 from 107 to get 77. Then multiply 10 *3= 30 and subtract 30 from 77 to get 47. Then multiply 10*3 = 30 and subtract 30 from 47 to get 17. We then move down to the next easier number for kids, which is 5. 5*3 =15 and we subtract 15 from 17 to get a remainder of 2. Then you add up all of the number to get 45 with a remainder of 2.
Zero Pair Example
Zero Pair Example
5+ -3 = 2
1+1+1+1+1
-1+-1+-1
These cancel out to leave 1+1 = 2
These pairs are zero pairs
Bases
Base 10
Base 10
0,1,2,3,4,5,6,7,8,9
Base 9
Base 9
0,1,2,3,4,5,6,7,8
Base 8
Base 8
0,1,2,3,4,5,6,7
Base 7
Base 7
0,1,2,3,4,5,6,
Base 6
Base 6
0,1,2,3,4,5
Base 5
Base 5
0,1,2,3,4
Base 4
Base 4
0,1,2,3
Base 3
Base 3
0,1,2
Base 2
Base 2
0,1
Subtraction with blocks
Subtraction with Non-Base 10 with blocks
431eight - 43eight
For the number 431, the 1 is the units place, the 3 is for the longs, and the 4 is for the flats.
We start by placing 4 flats, 3 longs, and 1 unit onto a flat surface.
We then begin with the units. We cannot take 3 units away from 1. We must break a long down into units.
Now we have 4 flats, 2 longs, and 9 units. We can subtract the 3 units from the 9 units. We have 6 units left over.
We have 4 flats, 2 longs, and 6 units. We have to subtract 4 longs. To do that we must break down one of the flats.
We now have 3 flats, 10 longs, and 6 units. We can subtract the 4 longs from 10 longs. We then are left with 3 flats, 6 longs, and 6 units.
366eight is our answer
Converting any base to Base 10
Converting any base to Base 10
441three to Base 10
We start by creating a chart with the powers 3^0, 3^1, and 3^2. Then you match the place values of the numbers (441)
3^2 3^1 3^0
4 4 1
Then we create the equation
(4*9) + (4*3) + (1*1)
36 + 12 + 1
49
441three is 49 in Base 10
Converting from Base to 10 any base
Converting from Base 10 to any base
Example 235 to Base 4
Start with listing the 4 powers that are needed for the problem
4^3 = 64
4^2 = 16
4^1 = 4
4^0 = 1
Then see how many times the biggest number (64) goes into the base 10 number (235). In this case it is 3 times.
64*3 = 192
235-192 = 43
Then you move onto the next number (16). 16 can go into 43 2 times.
16*2 = 32
43-32 = 11
Then see how many times 4 can go into 11. 2 times.
4*2 = 8
11-8 =3
And finally see how many times 1 can go into 3. 3 times.
1*3 = 3
3-3 = 0
So 235 is 3223three.
The link will bring up more examples
Expanded form of Base 10
Expanded form of Base 10
For example:
3562 base 10
3000+500+60+2 is the expanded form
Another example:
5347 base 10
5000+300+40+7 is the expanded form