af Nassim Khoury 3 år siden
357
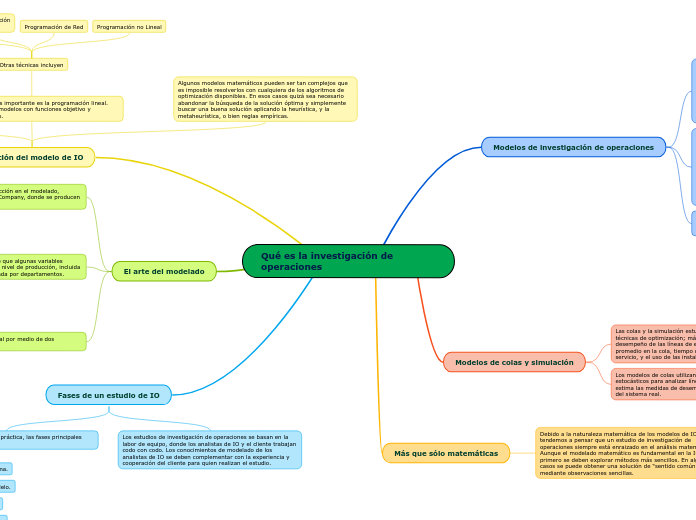
Qué es la investigación de operaciones
La investigación de operaciones se centra en la toma de decisiones informadas mediante el uso de modelos matemáticos y análisis cuantitativo. En este contexto, se presentan tres alternativas de compra de boletos, cada una con diferentes configuraciones para optimizar los costos y adaptarse a las restricciones de tiempo.