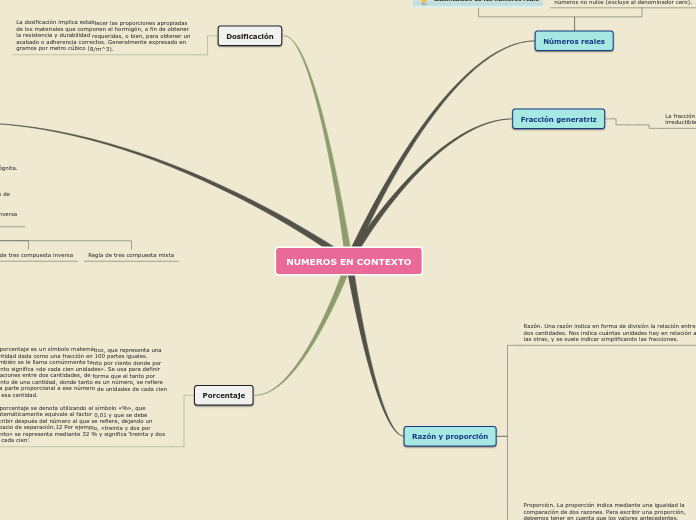
Sample Mind Map

Mere som dette

LASER

af Sofia Rosado

ética

af Magliz Javier

Proporcionalidad Directa

af Rodríguez, María Luisa

etapas de la historia de la filosofía

af daniel davd diaz bonilla

NUMEROS EN CONTEXTO

Porcentaje

El porcentaje es un símbolo matemático, que representa una cantidad dada como una fracción en 100 partes iguales. También se le llama comúnmente tanto por ciento donde por ciento significa «de cada cien unidades». Se usa para definir relaciones entre dos cantidades, de forma que el tanto por ciento de una cantidad, donde tanto es un número, se refiere a la parte proporcional a ese número de unidades de cada cien de esa cantidad. El porcentaje se denota utilizando el símbolo «%», que matemáticamente equivale al factor 0,01 y que se debe escribir después del número al que se refiere, dejando un espacio de separación.12 Por ejemplo, «treinta y dos por ciento» se representa mediante 32 % y significa ‘treinta y dos de cada cien’.

Regla de tres

La regla de tres es una forma de resolver problemas de proporcionalidad entre tres valores conocidos y una incógnita. En ella se establece una relación de linealidad (proporcionalidad) entre los valores involucrados. Regla de tres es la operación de hallar el cuarto término de una proporción conociendo los otros tres.123 La regla de tres más conocida es la regla de tres simple directa, aunque también existe la regla de tres simple inversa y la regla de tres compuesta.

Regla de tres compuesta mixta

Regla de tres compuesta inversa

Regla de tres compuesta directa

Regla de tres simple inversa

Regla de tres simple directa

Dosificación

La dosificación implica establecer las proporciones apropiadas de los materiales que componen el hormigón, a fin de obtener la resistencia y durabilidad requeridas, o bien, para obtener un acabado o adherencia correctos. Generalmente expresado en gramos por metro cúbico (g/m^3).

Razón y proporción

Proporción. La proporción indica mediante una igualdad la comparación de dos razones. Para escribir una proporción, debemos tener en cuenta que los valores antecedentes, siempre estén del mismo lado, al igual que los consecuentes.

En nuestro ejemplo del salón de clases, podemos comparar la razón que tenemos, de 4 niñas por cada 3 niños, y podremos calcular cuántos niños hay en un salón en relación al número de niñas o viceversa. Para esto, en primer lugar escribiremos la proporción que ya conocemos: 4:3 Después, un signo de igualdad 4:3= Y después la cantidad total, por ejemplo la del mismo salón, recordando que debemos respetar el orden del antecedente y del consecuente. En nuestro ejemplo, el antecedente será el número de niñas, y el consecuente el número de niños. 4:3=24:18 Para comprobar la igualdad de la proporción, se efectúan dos multiplicaciones. En una proporción, tomaremos como referencia el signo de igualdad. Los números que están más cercanos, se llaman centros, y los números más lejanos son los extremos. En nuestro ejemplo, los números 3 y 24 son los más cercanos al signo igual, por lo que son los centros. El 4 y el 18, son los extremos. Para comprobar que la proporción es correcta, el producto de la multiplicación de los centros debe ser igual al producto de la multiplicación de los extremos:3 X 24 = 72 4 X 18 = 72

Razón. Una razón indica en forma de división la relación entre dos cantidades. Nos indica cuántas unidades hay en relación a las otras, y se suele indicar simplificando las fracciones.

Por ejemplo, si en un salón de clases tenemos 24 niñas y 18 niños, entonces lo representaremos de alguna de las siguientes formas: 24/18 24:18 Y como la fracción podemos simplificarla al dividirla entre 6, entonces tendremos: 4/3 4:3 Y se lee que existe una razón de 4 a 3, o de 4 por cada 3. Cada uno de los valores de una razón tiene un nombre. El valor que está del lado izquierdo de la relación, se le llama antecedente, y al valor del lado derecho se le llama consecuente. En este caso, la relación de niñas respecto a los niños es una relación de 4 a 3, o de 4 niñas por cada 3 niños.

Fracción generatriz

Números reales

El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo cero, y a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos (excluye al denominador cero).

Clasificación de los números reale