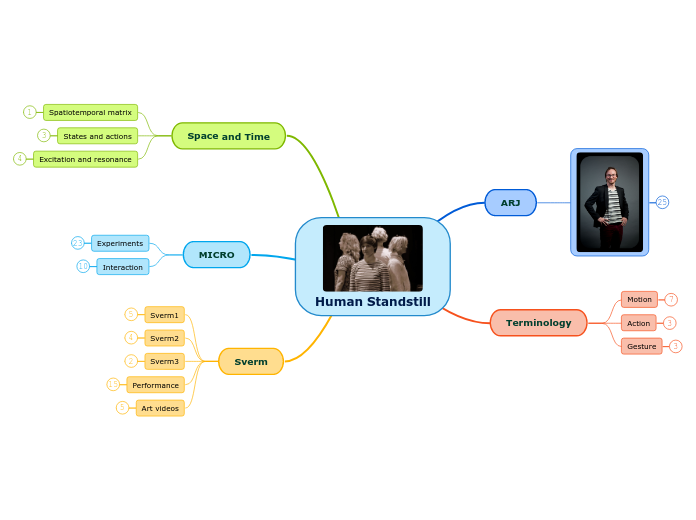
Fractions across Strands and Grades (Laura)
Collaborative action research shows: exploring fractions in a punctuated, or chunked, fashion throughout the school year is better for student understanding, rather than within a discrete unit.
- Punctuated instruction: allows teachers to be responsive to student thinking in 2 ways
- When planning subsequent activities.
- Students connect fraction knowledge when learning other mathematical concepts.
- Helps narrow focus of learning to the "key" concepts in fractions and slows down the learning so that students can spend the necessary time needed on tasks (one or multiple connected).
Curriculum: Specific at each grade level. When teachers have a deep understanding, they can better identify the embedding of fraction constructs in the math curriculum and identify student thinking that is "outside of the box" but still mathematically correct.
Better understanding = highly supports students to connect knowledge to learning outcomes desired in curriculum.
I like the idea of exploring fractions throughout the school year instead of sticking to one set unit. I think this would allow the students to "stay fresh" with their knowledge and understanding of fractions throughout the year, whereas keeping it in one unit could cause them to lose their knowledge over time. Also, I think that exploring fractions throughout the school year could allow the students to view fractions from different perspectives and use them in different ways that that may not do otherwise if they are only working with fractions in one set unit.
Ministry Resources (Laura)
Fractions Research: ALL Links available in document*
- Professional Learning about Fractions: A Collaborative Action Research Project Digital Paper (documents learning process of collaborative action research teams in Ont., lessons learned, & effective practices to inform thinking and development of future resources)
- Foundations to Learning and Teaching Fractions: Addition and Subtraction (lit. review, synthesizing existing knowledge from educational research)
- Math for Teaching: Ways We Use Fractions
- Math Teaching for Learning:
- 1 page synopses of key learnings from Foundations to Learning and Teaching Fractions
- Math Teaching for Learning
- Developing Fraction Number Sense
- Purposeful Representations
- Developing Proficiency with Partitioning, Iterating and Disembedding
- Building Understanding of Unit Fractions
- Building to Addition and Subtraction of Fractions
- Results of Collaborative Action Research on Fractions, KNAER Project
- Other Fraction Resources
"Paying Attention" to Documents:
- Proportional Reasoning
- Avail. in Adobe Presenter
- Spatial Reasoning
Webcasts:
- Planning for Mathematical Understanding: Fractions across the Junior Grades (journey of junior teachers planning and delivering a unit on fractions)
- Learning Mathematics within Contexts (Dr. Cathy Fosnot & a math study group, Gr. 6 classroom)
Guides to Effective Instruction:
- K- Gr. 6 Number Sense and Numeration
- Gr. 4-6 Fractions
- K- Gr. 3 Number Sense and Numeration
Student Digital Resources:
- Fraction: Exploring Part/Whole Relationships (interactive activities, games, quizzes, & learning tools with feedback)
- Learning Tools (collection of digital tools to explore fraction concepts)
- Gap Closing ePractice (digital interactive mathematic activities)
Section 004
Group #5
Paying Attention to Fractions
4 CONSTRUCTS
Part-Whole Relationship (Lydia)
- Learners are most familiar with this form
- the denominator indicates the fractional unit being used, and the numerator indicates the number of fractional units being counted.
Part-Part relationship (Lydia)
- we have limited practice, as this shows improper fractions, and we in classrooms over emphasize the use of proper fractions
-the digit in the denominator indicates the number of items that are in one part of the set, and the digit in the numerator indicates the number of items that are in the other part of the set
-The fractional unit, or number of equi-partitions of the whole, is determined by adding the digits in the numerator and denominator together.
Operator (Lydia)
- use of a fraction to enlarge or shrink a quantity.
- As students work with large numbers, they may see the connection to multiplication
Quotient (Lydia)
-construct of fractions relates to the notion of dividing the numerator by the denominator; which results in a decimal.
- students are initially exposed to the quotient construct through equal-share contexts.
- Can be shown multiple ways.
3 Models
Set Model (Richard)
A collection of various items represents the whole amount. Any subset of the whole creates the fractional part.
Representing Part-Part Relationships
First refer to Part-Part Relationships.
In the same fruit example as above, there are 3 pears and 6 fruits that are not pears. This can be represented as 3/6. It does not represent that there are 6 pieces of fruit and half are pears. It actually represents the ratio of pears to non pears. Since 9 is the total amount of pieces of fruit, there are 3 pears for every 6 pieces of fruit. The numerator represents one part of the whole, the denominator represents the other part of the whole.
Part-part relationships: ratio situations in which separate quantities are compared.
Representing Part-Whole Relationships
First Refer to Part-Whole Relationships.
Ensure to outline what constitutes a whole.
Ex 1:
3/2 cartons of eggs are full. A whole in this case is a full carton of eggs that contains 12 eggs. There are 12 eggs in one carton, and 6 eggs in another carton.
Ex 2:
A bunch of fruit is laid out: 3 pears, 2 oranges, 2 apples, 1 strawberry, 1 banana. The whole is that there are fruits laid out.
7/9 of the set are not oranges.
In this example, any attribute can be considered. An attribute is a qualitative or quantitative characteristic.
Part-whole relationships: situation in which a part is compared to a total amount.
Fraction: 2 components --> part and a whole.
Numerator: represents how many parts are included in the particular fraction.
Denominator: represents the whole of the parts.
This is easily represented using an area model*
Example: Many people sleep a total of 8 hours a night. The relationship of sleeping hours to total hours in a day is 8/24, which can be reduced to 1/3.
Linear Model (Samantha)
Linear Model is also known as a Number Line model.
Part-Part Relationships
Number Line Model Representing Part-Whole Relationships:
- in part-part relationships, the digit in the denominator indicates the number of items that are in one part of the set, and the digit in the numerator indicates the number of items that are in the other part of the set
- An example of this relationship modelled on a number line is the following:
- a vertical number line shows a part-part relationship in which the distance a flag has been hoisted up a pole is 3/2 of the distance left to be hoisted
- for every 3 segments hoisted there are two segments left to be hoisted
- arrow displaying the 3 segments hoisted, second arrow displaying the 2 segments left to be hoisted (see p. 7 of document for this example)
Part-Whole Relationships
Number Line Model Representing Part-Whole Relationships:
- in part-whole relationships, the digit in the denominator indicates the fractional unit that the whole has been divided into
- a fraction on a number line is an example of a part-whole relationship
- in a case of 0-1 on a number line, the whole is 1, with the fraction 7/9 being placed close to 1 (see p. 6 of document for this example)
Area Model (Erin)
· Area Model: is a continuous model in that one shape represents the whole. For example, a rectangle.
o This whole is divided into fractional regions, which are not necessarily the same size and shape.
· Area Models Representing Part-Whole Relationships:
o Denominator indicates the fractional unit being used -the number of equi-partitions that the whole has been divided into - while the numerator indicates the number of fractional units being counted.
o It is important to remember in a Part-Whole relationship, the denominator is not the whole number. For example: See email for visual representation.
3
2
o The denominator indicates the fractional unit is one-half (the whole is divided into halves). The whole is not 2.
o There are 3 one-halves indicated by the numerator, in this example.
o The whole is identified by the solid outlined rectangle. Fractions in both represent the shaded areas of the rectangles.
-Terminology: To partition an area model means to divide it into non-overlapping regions. For fractional units of the whole, the emphasis is on partitioning into equal-size regions or equi-partitioning.
· Area Models Representing Part-Part Relationships (describing the comparison between two things):
o Denominator indicates the number of items that are in one part of the set, and the numerator indicates the number of items that are in the other part of the set. The fractional unit (or number of equi-partitions of the whole), is determined by adding the digits in the numerator and denominator together.
o For example (p. 7):
7
2
o For every 7 shaded regions there are 2 unshaded regions: See email for visual representation.
· Operations Questions Using Area Model
o See document for subtraction example (p. 20).
o Word problem example: “There was 1/2 a pan of lasagna left. My dad ate 2/3 of the remaining lasagna, and my sister ate the rest. What fraction of the whole pan did my sister eat?”
o Here is a visual representation using Area: See email for visual representation.
o To solve this using an algorithm instead, you would first figure out that the sister ate 1/3 of the half-pan of remaining lasagna.
o Next you would determine that the question asked what fraction of the “whole pan did my sister eat?”.
o She ate 1/3 of 1/2
o You can then calculate the answer of 1/6
6 Type of Fractions (Richard)
All of the following types of fractions can incorporate negative (-) numbers in the numerator or denominator.
Mix Fractions
A quantity represented by an integer (whole number) and a proper fraction (See Proper Fraction).
Ex:
1 1/2
5 7/8
2 14/15
Complex Fractions
Either the numerator, denominator, or both are made up of fractions.
Ex:
3/4
7/8
2/5
7
4
6/11
Improper Fractions
Integers (whole numbers) are used in both the numerator and denominator. The numerator is greater than the denominator.
Ex: 5/2, 14/9, 7/3
It is beneficial to introduce students to improper or mixed fractions, together with proper and unit fractions so that students develop a sense of fraction as a number. When students are only presented with proper fractions, they may struggle when presented with fractions that challenge their current, limited understanding of what a fraction is. For example, if students interpret fractions to mean “out of,” such as 6/11 means 6 out 11, they may have difficulty understanding the meaning of 11/6, as this fraction doesn’t align with their current understanding of a fraction meaning “out of,” since having “11 out of 6” does not make sense. Therefore, it is important to help students develop a more holistic understanding of fractions by giving students experience with each type of fraction, rather than focusing mostly on proper fractions.
Unit Fractions
Integers (whole numbers) are used in the numerator and denominator, however the numerator is 1.
Ex: 1/2, 1/5, 1/27
Proper Fractions
There are whole numbers used in the numerator and denominator to represent a fraction. The numerator is less than the denominator.
Eg. 1/2, 3/5, 4/7, 7/8, 126/278
Simple Fractions
There are whole numbers used in the numerator and denominator to represent a fraction. The Denominator's cannot equal 0.
Eg: 1/2, 3/17, 7/9. 4/5, 17/8.
Simple fractions can include fractional units other than halves, thirds, fourths, etc. By providing opportunities to explore fractional concepts using a variety of fractions, including those that have “less friendly” denominators, student’s development of fraction number sense can become enhanced.
Comparing and Ordering/Solving Problems (Emily)
COMPARING AND ORDERING
- Many effective strategies to compare and order fractions besides finding the common denominator
- Number sense and proportional reasoning can be used to make comparisons once students develop a strong understanding of fractions (including multiplicative relationship between numerator and denominator)
- Constructing Models to make Comparisons
- Use number lines or rectangles to compare fractions
- Using Benchmarks to make Comparisons
- Number or measurement that is internalized and used to help judge other numbers or measurements
- “3 is less than half of 7, so 3/7 is less than ½” This shows an understanding of the multiplicative relationship between denominator and numerator
- Using Common Numerators to make Comparisons
- When numerators are common, such as in the fractions 7/11 and 7/13, students might reason at first that these fractions are equal
- Further investigation is required for students to understand that 7/11 is larger than 7/13
- Using Equivalent Fractions to Compare Fractions
- Use knowledge of equivalent fractions to create common numerators, and then compare the fractions
- Determining the equivalent fraction for one fraction involves simpler calculations than determining a common denominator
- Example: When comparing 3/11 to 6/19, students can find an equivalent fraction for 3/11 that will give them a common numerator with 6/19. In this case, the equivalent fraction of 3/11 would be 6/22. They can then compare 6/19 and 6/22.
- Using Unit Fractions to Order Fractions
- Students may find the fractional unit between the numerator and denominator of each fraction in question
- They may also determine which fraction is smaller, which will then tell them that this fraction will be closer to 1 since less of the whole is missing
OPERATIONS
- When students explore fraction concepts in a variety of ways, they develop an implicit understanding of addition, subtraction, division, and multiplication
- These experiences begin in primary grades and continue through to the intermediate grades
- Students are introduced to formal algorithms for these operations in intermediate grades
- The foundational concepts learning in elementary school are extended to algebraic expressions and to applications of fractions in contexts such as trigonometric ratios, radian measure, and probability in secondary school
IMPLICIT LEARNING
- Students use an addition statement to communicate their thinking when decomposing a part-whole fraction into a unit fraction
- When looking at the fraction 5/11, students may see this fraction as:
- On a number line
- Composed by counting “1 one-elevenths, 2 one-elevenths, 3 one-elevenths, 4 one-elevenths, 5 one-elevenths”
- Written as 1/11 + 1/11 + 1/11 + 1/11 + 1/11 = 5/11
- Describe as 5 one-elevenths or 5 x 1/11
- By seeing these connections when looking at the fractions, students develop an understanding for the roles of the numerator (count) and denominator (fractional unit) and understand that for both multiplication and addition, the unit stays the same between the numerator and denominator
- Algorithms can be learned and developed after students have had opportunities to explore these connections from primary through to senior grades
- Decomposing a part whole fraction can also result in subtraction or division statements
- Ex. Looking at the fraction 6/4, students can say that 6/4 – 4/4 = 2/4
- Or 6/4 divided ½ = 3, and then describe it as “one half goes into 6/4 three times”
- When solving problems of equal sharing, young students reason with fractions as operators, or multiplication by a fraction
SOLVING PROBLEMS
- Try to use visualizations as opposed to an algorithm
- Example question:
- “There was 12 a pan of lasagna left. My dad ate 23 of the remaining lasagna, and my sister ate the rest. What fraction of the whole pan did my sister eat?
- Using an algorithm may make solving this problem much more complicated than it would be if you used pictures. If using an algorithm, you would have to figure out what fraction of the half pan did the sister eat (which is 1/3), and you would have to realize that the question is asking you what portion of the whole 1/3 of ½ is, giving you the expression of 1/3 x ½
- Important to understand what type of fraction is being used in a question before performing the operation
For my section (4 constructs); they show each of them using a visual representation. I believe they are vital for understanding of the question so the students are even able to solve the problem. Therefore, using both a visual and the algorithm is an effective strategy for students, especially in the beginning when they start to figure out a part/whole relationship. (Lydia)
I agree Richard, I brainstormed a couple different ways I would interpret that application question, which I imagine is okay/reasonable as long as students can support their thinking and reasoning behind their responses. I actually think that asking students to represent or approach this question in more than one way would show higher level thinking and flexibility in their knowledge and understanding of fractions.
Your third answer is interesting because it requires students to first, determine what 1/3 means (represented by one apple and one pear, respectively), create two other groups that look like this (one apple and one pear and one additional fruit that is neither an apple or a pear), and then they can regroup to organize the same fruits together.
I was trying to consider ways that I would put this question into more student friendly language to prompt different responses but still make the question clear, for example: "These 2 fruits are one group out of 3 groups. What could the other two groups look like?".
The Set Model can be used with Unit Fractions where there are an equal number of items in each part. Related to the Fruit question that's listed under the part-whole sub topic under the set model topic shows there are 9 various fruits, 3 of the fruits are pears.When splitting the 9 fruits into equal groups to accommodate the pears, it shows 1/3 of the whole are pears.
Some other example questions that are listed are 'What fraction of the fruits are bananas?".There is 1 banana, and 9 fruits altogether. 1/9 of the fruits are bananas.
There is also an application/thinking question that shows a pear, and an apple and asks "if these fruit pieces represent 1/3 of the set, what might the set have been." This question seems confusing to me because I believe there are 2-3 answers.
Answer 1: a pear and an apple=1/3 of the set=2 pieces of fruit. 2+2+2=6. There are 6 pieces of fruit in the set, but the other 2/3 of fruit (4 pieces of fruit) can be fruits other than apples or pears.
Answer 2: the question asks if these fruit pieces represent 1/3 what might the set be. So my reasoning is that apples are 1/3 of the set, and pears are 1/3 of the set. Another fruit would be 1/3 of the set, so there are 3 fruits in the set.
Answer 3: A combination of the previous answers. An apple and a pear=1/3 of the set=2 pieces of fruit, but also apples=1/3 of the set, and pears=1/3 of the set. So there would be 2 apples, 2 pears, and 2 pieces of other fruit to be 6 pieces of fruit in the set.
I'm unsure if I'm correct on any of this.