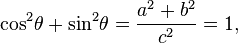Теорема Піфагора, Теорема Фалеса, теорема синусів і косинусів
Ця карта дасть інформацію про великих математиків та про важливі теореми геометрії.
Теорема Фалеса
Теорема Фалеса: якщо паралельні прямі, що перетинають дві задані прямі а і b, відтинають на одній прямій рівні відрізки, то вони відтинають рівні відрізки й на іншій прямій
Узагальнена теорема Фалеса
Узагальнена теорема Фалеса. Паралельні прямі, які перетинають сторони кута, відтинають від його сторін пропорційні відрізки.
На малюнку 172 прямі К1L1, К2L2 і К3L3 паралельні між собою. Тоді за узагальненою теоремою Фалеса:

З цієї пропорції можна зробити висновки:


Приклад. На малюнку 172  Знайдіть L2L3.
Знайдіть L2L3.
Розв’язання. К2К3 = К1К3 - К1К2 = 6 - 2 = 4 (см). За узагальненою теоремою Фалеса

Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на іншій його стороні.
Теорему Фалеса використовують, щоб поділити відрізок на декілька рівних частин.
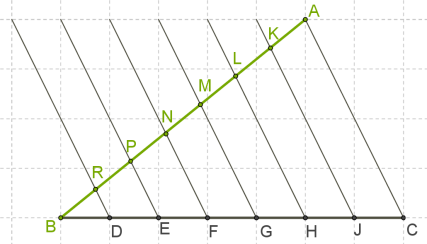
Необхідно поділити відрізок AB на 7 рівних частин.
Намалюємо кут, на одній стороні якого лежить відрізок AB.
Сторону кута BC намалюємо по клітинках і використаємо клітинки для поділу сторони на 7 рівних частин:
BD=DE=EF=FG=GH=HJ=JC
Кінці обох відрізків з'єднаємо, отримаємо AC. Проведемо прямі, паралельні AC, що починаються в точках J,H,G,F,E,D, отримаємо 7 паралельних прямих (знову використовуємо клітинки).
Якщо BD=DE=EF=FG=GH=HJ=JC і AC ∥ JK ∥ HL ∥ GM ∥ FN EP∥DR,
то за теоремою Фалеса, BR=RP=PN=NM=ML=LK=KA.
Теорема Фалеса. Теорема про пропорційні відрізки.
Фалес Мілетський
Фалес Мілетський — один із семи великих мудреців, «батько грецької науки», а також один з перших відомих в історії математиків. Він народився і жив в іонійському місті Мілеті на малоазійському узбережжі. Іонія з її м'яким теплим кліматом і родючим грунтом, вигідним географічним положенням на перехресті торгових шляхів з Азії і Африки в Європу в VII—VI ст. до н. е. стала домінуючою країною басейну Егейського моря.
Шумеро-вавілонська і єгипетська математика
Шумеро-вавілонська і єгипетська математика — вершини першого періоду розвитку математичного знання. Два основні математичні тексти Стародавнього Єгипту — папірус Ахмеса (переписаний у XVIII ст. до н. е. з тексту XX—XIX ст. до н. е.) і Московський (переписаний в XVIII—XVI ст. до н. е.) — містять відповідно 84 і 25 задач і свідчать про великий обсяг математичних знань. Єгипетські переписувачі того часу знали чотири арифметичні дії над натуральними числами і дробами виду — 1/n. Вони розв'язували задачі на арифметичні та геометричні прогресії, пропорційний поділ. Задачі на обчислення «аха» (купи, кількості) були першими задачами абстрактного характеру, з яких пізніше сформувалася алгебра. Чимало задач мають прикладний характер — на обчислення кількості хліба, який можна випекти з даної кількості зерна; кількості робітників, потрібних для виконання певної роботи, продуктів, щоб прогодувати працюючих, та ін.
Площі трикутника, прямокутника і трапеції вони вже обчислювали за точними відомими нам формулами, а площу круга — з точністю, якій відповідає добре наближення для числа π: π≈4 • (8/9) 2= 3,1605... . Вершиною єгипетської геометрії є обчислення об'єму правильної зрізаної чотирикутної піраміди за точною формулою. Уже з цього далеко не повного переліку можна зробити висновок, як багато різних математичних алгоритмів розв'язування задач, у тому числі і досить складних, знав або принаймні мав знати єгипетський писець того часу.
Ще більшими були досягнення шумеро-вавілонських математиків. Вони створили хоча ще й не послідовну, шістдесяткову позиційну систему числення, розробили алгоритми виконання чотирьох арифметичних дій над натуральними числами і дробами, записаними в цій системі.
Були виявлені в формі задач найпростіші типові зв'язки між величинами; своєрідною праалгеброю стали створені вавілонянами і єгиптянами деякі загальні методи розв'язування арифметичних задач. З великого числа уявлень і понять людина виділила три центральні поняття: поняття фігури, числа й величини — і сформувала деякі класи геометричних фігур. Вавілоняни впевнено розв'язували квадратні рівняння та їх системи, окремі рівняння вищих степенів, широко використовували теорему Піфагора до розв'язування геометричних задач практичного характеру.
Математична думка пройшла вже величезний шлях і відкрила надзвичайно багато властивостей чисел, закономірностей і відношень різних просторових форм. Це був тривалий період збирання в процесі спостережень і експериментів емпіричного матеріалу. Але математики, як дедуктивної науки з характерними для неї ланцюгами логічно доводжуваних тверджень, створено ще не було.
Приблизно на такому самому рівні були математичні знання і в Стародавній Греції в VIII—VII ст. до н. е. Наприклад, в Єгипті Фалес вразив місцевих землемірів (гарпедонавтів — натягувачів вірьовки) тим, що визначив висоту піраміди не в найпростішому випадку, коли довжина тіні вертикально поставленої віхи дорівнює довжині самої віхи, а в загальному, скориставшись методом встановлення пропорційного відношення між трьома величинами, які можна виміряти, і шуканою величиною — висотою піраміди.
Система лічби була ще не досконалою. Аттична, або геродіанова, непозиційна нумерація була ієрогліфічною. Числа до 4 позначали вертикальними паличками, число 5 — символом Г, 10 — ∆, 100 — Н, 1000 —X, 10 000 —М.
До греків ні в кого не виникало потреби вимагати доведень справедливості очевидних математичних тверджень. Наприклад, про те, що діаметр ділить коло на дві рівні частини, що вертикальні кути або кути при основі рівнобедреного трикутника рівні. Ніхто не цікавився, чому саме так, а не інакше потрібно розв'язувати задачу
Життя Фалеса
На час життя Фалеса припадають соціальні революції в іонійських полісах. Поліси були невеликими країнами, які складалися з міста — столиці і прилеглих до нього земель. У процесі революційних переворотів політичну владу в рабовласницької родової аристократії забирала заможна олігархія, а іноді й рабовласницька демократія. Ці соціальні зрушення сприяли духовному і культурному розвитку суспільства, одним з виявлень якого була діяльність самого Фалеса Мілетського, родоначальника античної і європейської науки, засновника стихійноматеріалістичної мілетської натурфілософської школи. Він був виключно обдарованим і різностороннім ученим — займався політикою, технікою, філософією, астрономією, математикою, торгівлею. Фалес, за переказами, був автором творів на природничі і філософські теми, але жодного рядка з них до нас не дійшло.
Офіційних посад учений не займав, хоч прославився як політичний діяч своїми далекоглядними рекомендаціями з питань військової тактики. Як інженер Фалес відомий тим, що за його порадою для форсування річки провели канал, у який тимчасово відвели її русло. Воїни перейшли річку, не замочивши й ніг. Знаменитий давньогрецький історик Геродот (бл. 485—бл. 425 до н. е.) писав у своїй «Історії», що під час битви між лідійцями і мідянами на прикордонній річці Галісі «день перетворився на ніч». Воїни так налякалися, що відмовилися воювати, і ворогуючі сторони помирилися. Сонячне затемнення в тому році завбачив лідійцям Фалес. Сучасні обчислення свідчать, що йдеться про затемнення 28 травня 585 р. до н. е.
Почесне місце займає Фалес в історії філософії. Першоосновою всього він вважав матеріальне начало — воду, а це було справжньою революцією в поглядах на світобудову.
Ім'я Фалеса стоїть першим і в історії математики. За даними більшості джерел родоначальники грецької науки свої наукові знання здобували, подорожуючи в Фінікію, Вавілон, Єгипет. З'ясуємо коротко, які ж математичні знання греки могли вивезти звідти.
Історія одного вченого
Піфагор
Піфагор Самоський (лат. Pythagoras; бл. 569-475 рр. до н.е.) — старогрецький філософ і математик, релігійний та політичний діяч, творець релігійно-філософської школи піфагорійців.
ФІЛОСОФСЬКЕ ТА РЕЛІГІЙНЕ ВЧЕННЯ
Вчення Піфагора варто розбити на дві складові: науковий підхід до пізнання світу і релігійно-містичний спосіб життя. Достеменно невідомі заслуги Піфагора в першій частині, оскільки йому пізніше приписували все, створене послідовниками в рамках школи пифагореизма. Друга частина превалює у вченні Піфагора, і саме вона залишилася в свідомості більшості античних авторів.
У збережених роботах
Аристотель
ніколи прямо не звертається безпосередньо до Піфагора, а лише до «так званих піфагорійців». У втрачених роботах (відомих за витягами) Аристотель розглядає Піфагора як засновника напіврелігійного культу, котрий забороняв їсти боби і мав золоте стегно, але не належав до когорти мислителів, попередників Аристотеля.
Платон ставився до Піфагора з найглибшою пошаною і повагою. Коли піфагорієць Філолай уперше опублікував три книги, де викладені основні положення піфагореїзму, Платон за порадою друзів негайно їх купив за великі гроші.
Діяльність Піфагора як релігійного новатора VI ст. до н.е. полягала у створенні таємного товариства, яке не лише ставило перед собою політичні цілі (через що піфагорійців розгромили в Кротоні), але, головним чином, звільнення душі шляхом морального та фізичного очищення за допомогою таємного вчення (містичне вчення про кругообіг переселень душі). За Піфагором, вічна душа переселяється з небес у тлінне тіло людини або тварини і зазнає ряд переселень, поки не заслужить права повернутися назад на небеса.
В акусматах (висловах) Піфагора містяться обрядові настанови: про кругообіг людських життів, поведінці, жертвоприношеннях, похованнях, харчуванні. Акусмати сформульовані лаконічно і доступно для розуміння будь-якої людини, в них містяться також постулати загальнолюдської моралі. Складніша філософія, в рамках якої розвивалася математика та інші науки, призначалася для «посвячених», тобто обраних людей, гідних володіти таємним знанням. Наукова складова вчення Піфагора розвивалася в V ст. до н.е. зусиллями його послідовників (Архіт з Тарента, Філолай з Кротона, Гіппас з Метапонта), але зійшла нанівець у IV ст. до н.е., у той час як містично-релігійна складова отримала свій розвиток і друге народження у вигляді неопіфагореїзму за часів Римської імперії.
Життя Піфагора
За словами античних авторів, Піфагор зустрівся мало не з усіма відомими мудрецями тієї епохи — греками, персами, халдеями, єгиптянами, — ввібравши в себе все накопичене людством знання. У популярній літературі іноді приписують Піфагору Олімпійську перемогу в боксі, плутаючи Піфагора-філософа з його тезкою (Піфагором, сином Кратета з Самоса), який здобув свою перемогу на 48-х Іграх за 18 років до народження знаменитого філософа.
До вавилонських магів і халдеїв Піфагор потрапив вже проти своєї волі — як полонений перського царя Камбіза, котрий завоював на той час Єгипет. Там мандрівник прожив 12 років, перейнявши у халдеїв релігійні таїнства та математичні знання.
Переказують, що він побував і в Індії, де спілкувався з брахманами, від яких засвоїв не лише філософію, зокрема вчення про переселення душ, а й секрети вправ для тіла.
Повернувшись у Грецію на п’ятдесятому році життя, Піфагор оселився на півдні італійського півострова — у грецькій колонії Кротоні, де знайшов багато послідовників. Їх приваблювала не лише містична філософія, яку він переконливо викладав, але й приписуваний ним спосіб життя з елементами здорового аскетизму і суворої моралі. Піфагор проповідував моральне облагороджування неосвіченого народу, досягти якого можливо там, де влада належить касті мудрих і знаючих людей, і яким народ кориться в чомусь беззастережно, як діти батькам, а в іншому свідомо, підкоряючись моральному авторитету.
Учні Піфагора утворили свого роду релігійний орден — гетерію — прообраз майбутньої філософської школи. Це було братство посвячених, що складалося з касти відібраних однодумців, які буквально обожнювали свого вчителя — засновника ордена. Незабаром і в інших полісах південної Італії та Греції виникли піфагорійські гетерії, в яких поряд з науковими проблемами — математичними, філософськими, етичними — розглядалися релігійні й політичні.
Цей орден фактично прийшов у Кротоні до влади, однак через антіпіфагорейскі настрої наприкінці VI ст. до н.е. Піфагору довелося втекти в іншу грецьку колонію Метапонт, де він і помер близько 475 р. до н.е.
Дитинство
Історичні дослідження датують появу Піфагора на світ приблизно 569 роком до нашої ери. Народився Піфагор на острові Самосі, біля узбережжя Малої Азії. Його батько Мнесарх із знатного, але збіднілого роду, був каменерізом. Згідно з легендою, Мнесарх звернувся до Піфії з приводу однієї дуже важливої для нього подорожі. Він отримав відповідь, що подорож буде успішною, а його дружина народить дитину, яка буде виділятися з-поміж усіх, хто жив коли-небудь, красою й мудрістю, і принесе людському роду дуже велику користь на всі часи. Після пророцтва Мнесарх дав своїй дружині нове ім’я — Піфаїда, а новонародженому — Піфагор, яке означає «той, про кого оголосила Піфія».
Батько дав Піфагору добру освіту, навчаючи його в найбільш знаменитих учителів того часу. Багато хто вважав, що він — син бога Аполлона. Після смерті батька Піфагор вирушає до Мілета, де його вчителями були Ферекід, Анаксімандр і Фалес. Саме за порадою Фалеса 20-річний Піфагор їде до Єгипту, щоб набратися мудрості і таємних знань у єгипетських жерців. Діоген і Порфирій пишуть, що Самоський тиран Полікрат забезпечив Піфагора рекомендаційним листом до фараона Амасіса, завдяки чому він був допущений до навчання і посвячений у таїнства, заборонені для інших чужинців. У Єгипті він прожив близько 22-х років і витримав немало випробувань, перш ніж жерці Мемфіса і Діосполіса відкрили йому «дивовижне чергування чисел, хитромудрі правила геометрії, науку про зорі, медицину».
Теорема Піфагора
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.Графічно це можна зобразити так: а² + b ² = c²
Наслідки з теореми Піфагора
Одним з наслідків теореми Піфагора є те, що відрізки на лінії, довжина яких є неспівмірною, можуть бути побудовані за допомогою
лінійки та циркуля.
Теорема Піфагора дозволяє побудувати неспівмірні довжини через те, що гіпотенуза трикутника пов'язана з його сторонам через корінь квадратний. Малюнок справа демонструє як побудувати відрізки, довжина яких у співвідношенні дає корінь квадратний будь-якого цілого числа. Кожен трикутник має сторону (позначену «1»), довжина якої є вибрана одиниця вимірювання. На кожному прямокутному трикутнику завдяки теремі Піфагора отримуємо довжину гіпотенузи виражену у вибраних одиницях. Якщо гіпотенуза пов'язана з одиницею вимірювання через квадратний корінь з додатнім цілим числом, що не є піднесенням до квадрата, тоді ми отримуємо реалізацію неспівмірності для цієї одиниці. Наприклад, √2, √3, √5.
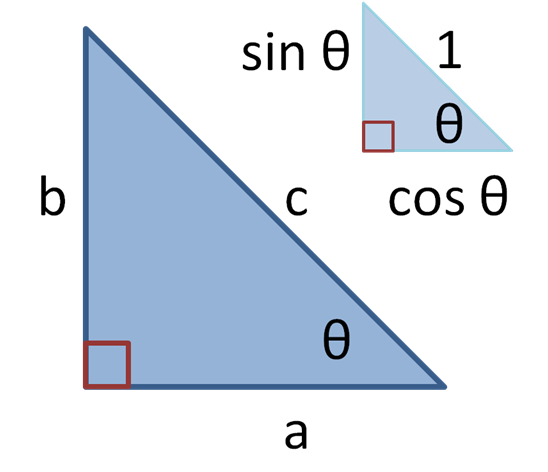
Для прямокутного трикутника із сторонами a, b та гіпотенузою c, запишемо тригонометричні визначення синуса і косинуса кута θ між стороною a та гіпотенузою:

звідси випливає що:
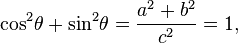
де в останньому кроці доведення застосовуємо теорему Піфагора. Цю залежність між синусом і косинусом іноді називають фундаментальною тригонометричною тотожністю Піфагора.
В подібних трикутників, співвідношення між сторонами рівне незалежно від розмірів трикутника, а залежить тільки від кутів. Відповідно, на рисунку зображено трикутник з гіпотенузою, яка дорівнює одиниці, сторона протилежна до кута дорівнює sin θ і прилегла сторона — cos θ в одиницях гіпотенузи
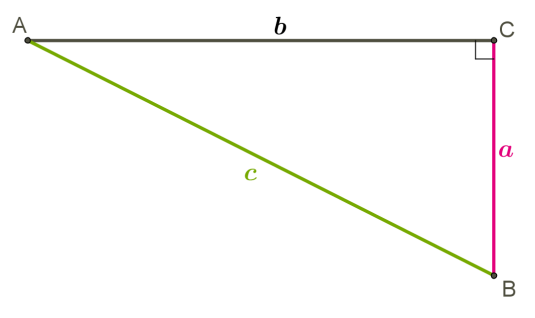
Площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на його катетах.
Одна з найвідоміших геометричних теорем — теорема Піфагора, знаменитого давньогрецького філософа і математика.
В історії математики знаходимо твердження, що цю теорему знали за багато років до Піфагора, наприклад, стародавні єгиптяни знали про те, що трикутник зі сторонами 3, 4 і 5 є прямокутним.
У наш час теорема звучить так (маючи на увазі не тільки площі, але і довжини сторін прямокутного трикутника):
Теорема косинусів
Теорема косинусів — це твердження про властивість довільних трикутників, що є узагальненням теореми Піфагора. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших його сторін без подвоєного добутку цих сторін на косинус кута між ними.
Доведення теореми косинусів
Доказ теореми косинусів

Розглянемо довільний трикутник ABC. Припустимо, що нам відома величина боку AC (вона дорівнює нікому числу b), величина боку AB (вона дорівнює нікому числу c) і кут між цими сторонами, величина якого дорівнює α. Знайдемо величину сторони BC (позначивши її довжину через змінну a)
Для доведення теореми косинусів проведемо додаткові побудови. З вершини C на сторону AB опустимо висоту CD.
Знайдемо довжину сторони AB. Як видно з малюнка, в результаті додаткового побудови можна сказати, що
AB = AD + BD
Знайдемо довжину відрізка AD. Виходячи з того, що трикутник ADC є прямокутним, нам відомі довжина його гіпотенузи (b) і кут (α) то величину сторони AD можна знайти із співвідношення його сторін, користуючись властивостями тригонометричних функцій в прямокутному трикутнику:
AD / AC = cos α
звідки
AD = AC cos α
AD = b cos α
Довжину сторони BD знайдемо як різницю AB і AD:
BD = AB - AD
BD = c − b cos α
Тепер запишемо теорему Піфагора для двох прямокутних трикутників ADC і BDC:
для трикутника BDC
CD2 + BD2 = BC2
для трикутника ADC
CD2 + AD2 = AC2
Звернемо увагу на те, що обидва трикутника мають загальну сторону - CD. Визначимо її довжину для кожного трикутника - винесемо її значення в ліву частину виразу, а решта - в праву.
CD2 = BC2 - BD2
CD2 = AC2 - AD2
Оскільки ліві частини рівнянь (квадрат сторони CD) рівні, то прирівняємо праві частини рівнянь:
BC2 - BD2 = AC2 - AD2
Виходячи із зроблених раніше обчислень, ми вже знаємо що:
AD = b cos α
BD = c − b cos α
AC = b (за умовою)
А значення сторони BC позначимо як a.
BC = a
(Саме його нам і потрібно знайти)
Отримаємо:
BC2 - BD2 = AC2 - AD2
Замінимо буквені позначення сторін на результати наших обчислень
a2 - ( c − b cos α )2 = b2 - ( b cos α )2
перенесемо невідоме значення (а) на ліву сторону, а решта частини рівняння - на праву
a2 = ( c − b cos α )2 + b2 - ( b cos α )2
розкриємо дужки
a2 = b2 + c 2 - 2c b cos α + ( b cos α )2 - ( b cos α )2
отримуємо
a2 = b2 + c 2 - 2bc cos α
Теорема косинусів доведена.
Випадок, коли один з кутів при підставі тупий (і висота падає на продовження основи), повністю аналогічний розглянутому.
Формулювання теореми косинусів
Формулювання теореми косинусів
Для плоского трикутника зі сторонами a, b, c і кутом α, протилежними стороні a, справедливо співвідношення:


Квадрат одного боку трикутника дорівнює сумі квадратів двох інших сторін за вирахуванням подвоєного їх твору, помноженого на косинус кута між ними
Корисні формули теореми косинусів:

Як видно із зазначеного вище, за допомогою теореми косинусів можна знайти не тільки сторону трикутника за двома сторонами і кутом між ними, можна, знаючи розміри всіх сторін трикутника, визначити косинуси всіх кутів, а також обчислити величину будь-якого кута трикутника. Обчислення будь-якого кута трикутника по його сторонах є наслідком перетворення формули теореми косинусів.
Теорема синусів
Теорема синусів стверджує, що відношення довжин сторін до синусів відповідних протилежних кутів є величина стала, отже

Наслідок з теореми синусів
Радіус описаного кола
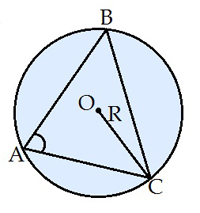
asinA=bsinB=csinC=2R, де R — радіус описаного кола.
Виразивши радіус, отримуємо R=a2sinA, або R=b2sinB, або R=c2sinC.
.
Теорія
Теорема синусів
Теорема синусів встановлює залежність між величиною кутів трикутника і протилежних йому сторін.
Формулювання теореми синусів
Сторони трикутника пропорційні синусам протилежних кутів
або,

де
R - радіус описаного навколо трикутника кола
a, b, c - сторони трикутника
α, β, γ - величини протилежних цим сторонам кутів
Доказ теореми синусів

Доказ теореми синусів відбувається за допомогою додаткових побудов.
Побудуємо довільний трикутник, вписаний в коло. Позначимо його як ABC.
Додатково побудуємо діаметр окружності, в яку вписаний довільний трикутник, але так, щоб він проходив через один з його кутів. Діаметр дорівнює подвійному радіусу кола (2R).
Візьмемо до уваги, що однією з властивостей прямокутного трикутника, вписаного в коло є те, що його гіпотенуза, є діаметром кола, в яке він вписаний.
Позначимо діаметр для описаного кола як BD. Утворений трикутник BCD є прямокутним, оскільки його гіпотенуза лежить на діаметрі описаного кола (властивість кутів, вписаних в коло).
Таким чином, додатково побудований трикутник, у якого одна загальна сторона з побудованим раніше довільним трикутником, а гіпотенуза збігається з діаметром окружності - є прямокутним. Тобто трикутник DBC - прямокутний.
Для доказу всієї теореми, оскільки розміри трикутника ABC обрані довільним чином, досить довести, що співвідношення однієї довільної сторони до протилежного їй кута одно 2R.
Нехай це буде 2R = a / sin α, тобто якщо взяти за кресленням 2R = BC / sin A.
Оскільки, кути, вписані в коло, що спираються на одну й ту ж дугу, рівні, то кут CDB або дорівнює куту CAB (якщо точки A і D лежать по одну сторону від прямої BC), або дорівнює π - CAB (в іншому випадку).
Звернемося до властивостей тригонометричних функцій. Оскільки sin (π - α) = sin α, то зазначені варіанти побудови трикутника все одно призведуть до одного результату.
Обчислимо значення 2R = a / sin α, за кресленням 2R = BC / sin A. Для цього замінимо sin A на співвідношення відповідних сторін прямокутного трикутника.
2R = BC / sin A
2R = BC / ( BC / DB )
2R = DB
А, оскільки, DB будувався як діаметр кола, то рівність виконується.
Повторивши той же міркування для двох інших сторін трикутника, отримуємо:

Відео з поясненням