von Diana Rodriguez Vor 3 Jahren
170
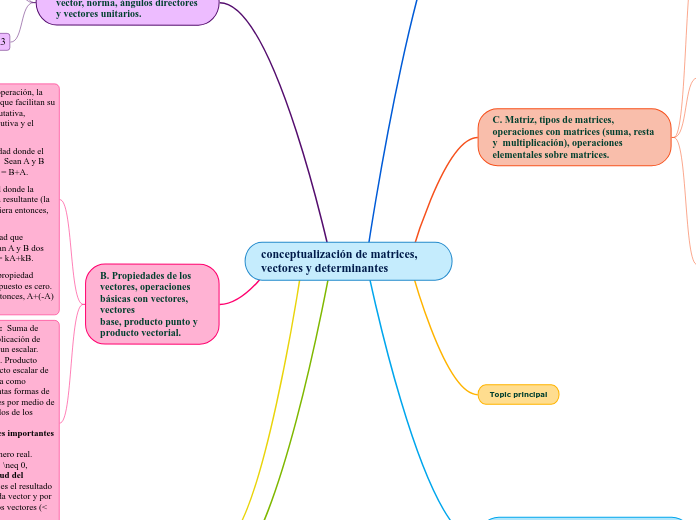
conceptualización de matrices, vectores y determinantes
La conceptualización de matrices, vectores y determinantes es fundamental en diversas áreas de las matemáticas y la física. Los vectores tienen propiedades cruciales como la conmutativa, asociativa y distributiva, especialmente en operaciones como la suma, resta y multiplicación.