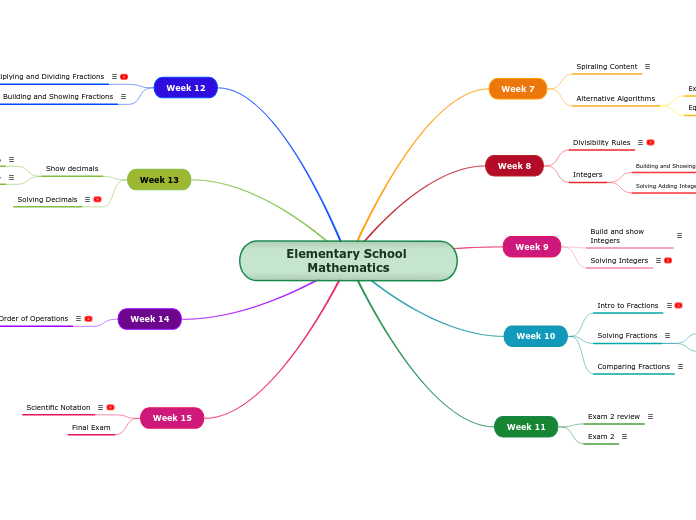
Elementary School Mathematics
Week 15
Final Exam
Scientific Notation
Teach students that they are either really big or really small numbers, multiplied by ten many times to make it more easily understood. They will also always be between 0-10 and teach that;
positive exponent=big number (1-10)
negative exponent=small number (0-1)
Week 14
Order of Operations
For order of operations, students need to learn that multiplying/dividing and adding/subtracting are interchangeable. Teaching both PEMDAS and PEDMSA. Teach students to break down problems and do them in parts. Do all Parentheses first, then exponents, do multiplication and division in left to right order, finishing with adding and subtracting left to right.
Week 13
Solving Decimals
Teach students to line up the whole number. Students may struggle if taught to line up the decimal, as not all numbers have decimals, while all numbers will have a whole number.
With. multiplication have students estimate the answer before attempting to multiply. Then have them multiply, and based off their estimate have them put the decimal back into the problem.
Show decimals
Multiply
Have student draw 100 square diagrams to solve multiplying decimal problems, spiraling back to how fractions were solved.
Add/sub
For adding and subtracting, spiral back to fractions and have students draw out diagrams to solve. Connect that decimals are fractions.
Week 12
Building and Showing Fractions
Students should practice drawing out diagrams of fractions in order to help them visualize and solve problems. They can draw the denominator and color in the numerator to help them solve. With multiplying they should draw a grid with one fraction vertical and one horizontal in and the answer will be the squares that are colored in by both colors.
Multiplying and Dividing Fractions
To multiply fractions, students need to factor out fractions, then cross reduce by making 1 pairs.
To divide fractions, students should follow a Keep Change Flip, where they keep the first fraction, change division to multiplication, and then flip the numerator and denominator of the second fraction.
Week 11
Exam 2
Test will cover content from weeks 7 through 10, and will be based on their ability to show their work in a comprehensive manner.
Exam 2 review
Students will be provided a study guide reviewing content from weeks 7 through 10 in order to help them review for the exam.
Week 10
Comparing Fractions
There are a variety of strategies to compare fractions with different denominators.
The first is the half test, where you double each numerator to see if it's more than the denominator.
You can also draw out the fractions and compare them that way.
If fractions have the same numerator the fraction with the smaller denominator would be the bigger fraction.
If they have the same denominator the larger numerator is bigger.
Solving Fractions
When we switch to solving adding and subtracting fractions, we should teach students a few different algorithms and avoid improper fractions at all costs.
Converting fractions to solve
We also have to teach students how to convert fractions, spiraling back to multiplication, in order to add and subtract fractions.
For Example: 1/2 + 3/8
2 can multiply by 4 to get 8, and when we multiple we have to multiply both parts, so we end up with 4/8 +3/8
Sometimes both sides must be multiplied, for example 1/4 + 2/3 would mean that you would need to multiply 4 by 3 and 3 by 4, giving you 3/12 + 8/12
Solving with whole numbers
One method with mixed numbers is to teach students that a whole number can be turned into a fraction for subtraction. For Example:
10 - 3/8 can be solved by turning 10 into 9 and 8/8, meaning you can subtract and get 9 5/8.
Intro to Fractions
Students will receive their first introduction to fractions.
The numerator should be introduced as the number of pieces of a whole you have, and the denominator should be introduced as how many pieces of the whole there are all together.
Examples are very helpful for building understanding, as students need to understand that a smaller number as the denominator is bigger than a larger number. Visual examples, such as slices of pizza, are a great way to build this understanding in students.
Week 9
Solving Integers
Students solving subtraction with integers can use the keep change change method to help with problems that can be confusing such as 3-(-4).
With this problem students would keep the 3 change the - to a + and change the negative 4 to a positive 4, leaving them with 3+4, a far less confusing problem.
For multiplication students learn the rule same sign equals a positive answer, different sign equals a negative answer. This allows them to solve a problem like -5(3) without worrying about the sign in the problem, as they know their answer will be a negative, and can just do 5(3), adding in the negative at the end, leaving them with -15. If the problem was -5(-3) they would have 15.
Build and show Integers
Using skills learned the week before, students learn to subtract and multiply integers.
Students learn to look at problems as take away with subtraction spiraling back and use their two sided counters to display problems.
Students learn for multiplication problems to see it as 0 takeaway x groups of (y). They also learn to look at problems as x groups of (-y).
For multiplication students learn the important rule, same sign equals a positive answer, different sign equals a negative answer. This will help them do problems without being tripped up by signs.
Week 8
Integers
Solving Adding Integers
Using the skills and tools from building integers, students will now use counters, or drawings to help represent and solve problems.
For Example:
4 + (-5) can be represented as
++++
- - - - -
These methods will help students visualize and solve problems with positive and negative numbers.
Building and Showing Integers
Building integers is extremely important to help students understand integers. The most helpful way to do this is to have two sided counters on hand for student use.
Zero Banks
Zero Banks are important for showing integers, as they help establish the concept of 0 as a number.
Students build zero banks by showing that a positive number and a negative number cancel out, so long as they are equal.
These are easily displayed using the colored counters used to build integers.
Divisibility Rules
It is important to explain to students how the divisibility rules work, as it will help with fractions, and these rules can be spiraled back to multiplication facts in some cases.
The Rules:
2: Even numbers
3: Add all numbers and divide by 3
4: Last two digits divide by 4
5: Ends in 5 or 0
6: Both 2 & 3 rules work
8: Last three digits divide by 8
9: All numbers add together to a number divisible by 9
10: Ends in 0
Week 7
Alternative Algorithms
Equal Addends
Equal Addends is a subtraction strategy that will be new to students, but may remind them of friendly numbers.
With equal addends you add the same number to both the number that is being subtracted from, and the number that is being subtracted to make it a simpler problem. This is especially useful to eliminate the need for borrowing during subtraction.
For example: 455-278, in order to simplify this problem you would add 22 to both numbers in order to get the problem
477
-300 which is far simpler to solve.
Expanded Form
Expanded form is a way to teach addition and subtraction. This should've been previously taught for addition and can be spiraled back to as part of your lesson.
Example: 567-342
500+60+7
-300+40+2
Spiraling Content
Spiraling content is the method of teaching a concept and coming back to it when a later topic relates. By spiraling your content and tying it together, you can help students build a deeper understanding, and help them relate concepts previously learned that will assist in whatever new concept is being added.
For Example:
If you're starting with multiplication facts you could spiral back to them during fractions, which will help them when they need to find least common denominators.