von Alfonso Jiménez del Val Vor 2 Jahren
156
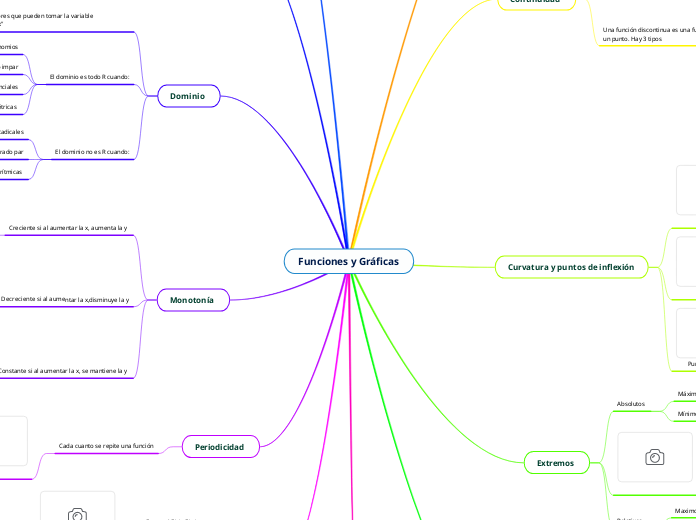
Funciones y Gráficas
Las funciones matemáticas representan relaciones entre dos variables, usualmente denominadas 'x' e 'y'. Al analizar estas funciones, se estudian diversos aspectos como su dominio, que es el conjunto de valores que puede tomar la variable independiente, y su recorrido, que abarca los valores que puede asumir la variable dependiente.