von Adnan Malik Vor 3 Jahren
196
Introduction To Functions
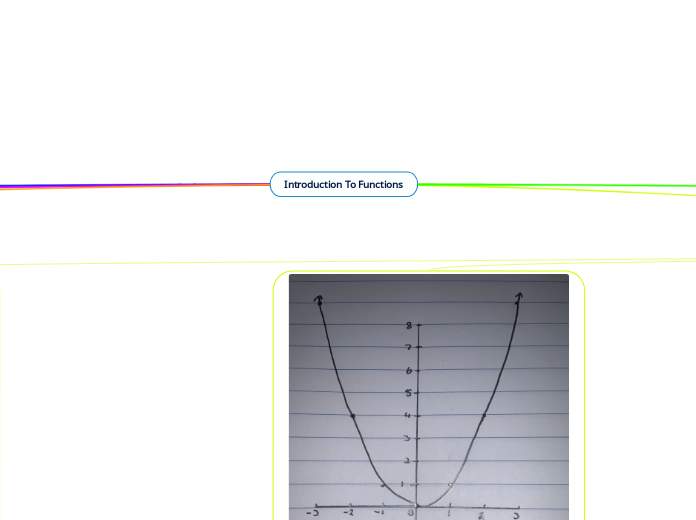
Functions are mathematical constructs where each input is associated with exactly one output. The domain of a function is the set of all possible input values, while the range is the set of all possible outputs.