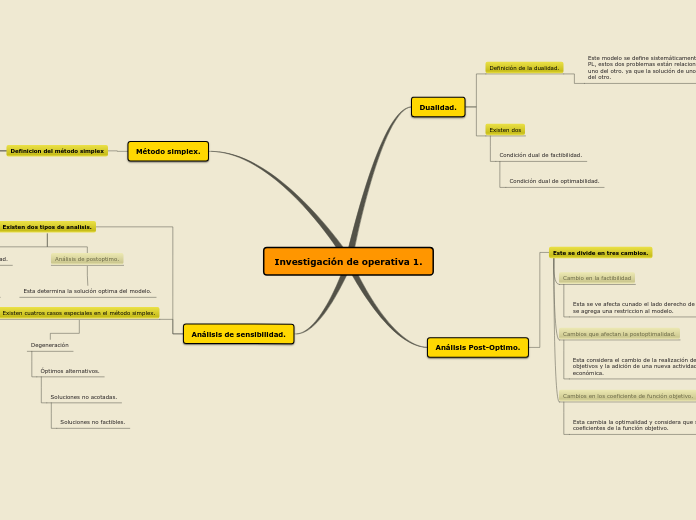
Investigación de operativa 1.
Análisis de sensibilidad.
Existen cuatros casos especiales en el método simplex.
Degeneración
Óptimos alternativos.
Soluciones no acotadas.
Soluciones no factibles.
Existen dos tipos de analisis.
Análisis de postoptimo.
Esta determina la solución optima del modelo.
Este determina
Método simplex.
Definicion del método simplex
Se utiliza operaciones de gauss - jordan para resolver este método, esto se lleva a cabo iterando las filas con las columnas para de esa manera obtener un resultado optimo.
Para la solución de este problema se necesitan dos restricciones en el programa lineal.
Todas las ecuaciones son restricciones con lado derecho no negativo.
Todas las variables son no negativas.
Es un método analitico de solución de problemas de programación lineal capaz de resolver modelos más complejos que los resultados mediante el método gráfico sin restricción en el numero de variable.
Análisis Post-Optimo.
Este se divide en tres cambios.
Cambios en los coeficiente de función objetivo.
Esta cambia la optimalidad y considera que se cambien los coeficientes de la función objetivo.
Cambios que afectan la postoptimalidad.
Esta considera el cambio de la realización de los coeficientes objetivos y la adición de una nueva actividad variable o económica.
Cambio en la factibilidad
Esta se ve afecta cunado el lado derecho de las restricciones o se agrega una restriccion al modelo.
Dualidad.
Existen dos
Condición dual de factibilidad.
Condición dual de optimabilidad.
Definición de la dualidad.
Este modelo se define sistemáticamente a partir del modelo PL, estos dos problemas están relacionados estrechamente uno del otro. ya que la solución de uno depende de la solución del otro.
Los coeficientes de la función objetivo en el problema dual corresponden a los términos independientes de las restricciones.
El número de restricciones que representa el problema dual, se ve determinado por el número de variables del problema.
El número de variable que representa el problema dual, se ve determinado por el número de restricciones del problema.
Entre estos dos existen algunas relaciones.