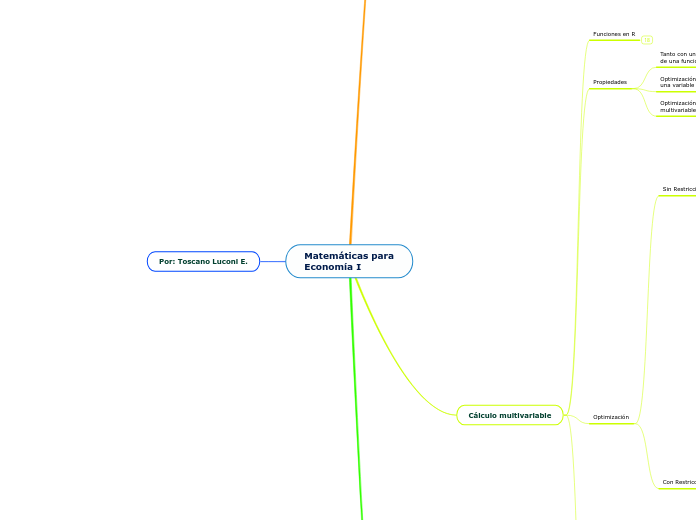
Matemáticas para
Economía I
Por: Toscano Luconi E.
Ecuaciones
Diferenciales
Ejemplos y Usos
Tipos de ED
Parciales (EDP): Son ecuaciones que contienen tanto derivadas ordinarias como derivadas parciales de las variables definidas.
Ordinarias (EDO): Son ecuaciones que solo contienen derivadas ordinarias, o sea no utilizan derivadas parciales.
Lineal (no lineal): Es una ecuación en la que el grado máximo de f(x) ( y sus diferenciales) es 1. Puede tener otros términos de grado superior, pero seguir siendo lineal en y.
Separable
Homogénea
Autonoma: Es una ecuación en la que la variable independiente no está de forma explicita.
Tiene forma de y' = y+c ; en vez de y' = y+x
Otros métodos de Solución
Método de Euler: Propone usar el valor inicial y rectas tangentes al campo direccional para encontrar una curva que se asemeja a la solución. Esto se obtiene al ir reduciendo el "tamaño de paso" de x para producir una solución acertada.
Utiliza una función linear para producir los nuevos pasos de la gráfica. Por ejemplo, para x=0.5, y=2x+0.5
Método de Euler
Matemáticamente
Campos Direccionales: Resultado de dibujar la pendiente de varias soluciones en un plano cartesiano. A un plano con las posibles pendientes se le conoce como campo direccional.
Estos segmentos de recta indican en que dirección apunta una curva de solución de la función.
Campo direccional de y' = x+y
Solución de ED: Es una función f que cuando se sustituye en otra ecuación con sus diferenciales (derivadas), da como resultado la igualdad y = f(x).
Condición Inicial: Es una situación de forma y(t0) = y0, en la cual se debe encontrar una solución que satisfaga la condición.
Solución General: Es una solución de f(x) de forma
y = x3/3 + C
Resolver una ED implica encontrar una función (o familia de funciones) que satisfacen la ecuación y sus condiciones iniciales.
Orden: Es el máximo grado de diferencial que contiene la ecuación.
2y' = 2y -> primer orden
y'' + y' = y -> segundo orden
d3y/dx = y -> tercer orden
Definición: Es un modelo en que sus variables se relacionan con sus derivadas, y sus variables suelen ser continuas.
La mayor parte toman el tiempo t como variable independiente, por lo que modelan el comportamiento de algo, con respecto al tiempo.
Cálculo multivariable
Curvas de Nivel
Son representaciones gráficas de 3 dimensiones, en un plano de 2 dimensiones. Generalmente se trabaja en el plano xy y da como resultado una serie de líneas que indica donde está el valor de la tercera variable dadas las otras.
Las aplicaciones más comunes son las Iscocuantas, Isocostos y las Curvas de Indiferencia.
Para obtener el plano xy en función de la variable z, se destina z como constante y se depejan los valores de las demás variables.
Subtopic
Optimización
Con Restricciones
Si una función está sujeta a una restricción (llámese producción está sujeta al presupuesto empresarial), se debe optimizar tomando en cuenta dichas limitantes. Los métodos más comunes son por Sustitución o por Multiplicadores de Lagrange
Se utiliza la Matriz Hessiana Orlada (variante de la Hessiana normal) para determinar qué tipo de punto crítico es.
La matriz es cuadrada y simétrica, pero su orden depende de la cantidad de variables de la función.
Criterios para más de 3 variables y una restricción, mediante análisis de determinante de submatrices.
1. Si todos son menores que 0, entonces es un mínimo.
2. Si el primer det|Ho| de 3x3 es > 0,
y el segundo de 4x4 < 0, y así sucesivamente, entonces el punto es un máximo.
3. Si todos los det|Ho| son distintos de 0, pero no siguen un orden definido, entonces es un punto de inflexión.
4. Si no se da ningun caso, el criterio no concluye nada.
Sus componentes no son funciones, sino que son evaluados en un punto crítico para determinar si es min, max o inflexión.
Se analizan los menores complementarios del HO:
En R2
Si |H3| = f(x,y,µ) < 0, entonces (x,y) es un min.
Si |H3| = f(x,y,µ) > 0, entonces (x,y) es un max.
En R3
Si |H3| = f(x,y,z,µ) < 0, y |H4|<0, (x,y,z) es un min.
Si |H3| = f(x,y,z,µ) < 0, y |H4|>0. (x,y,z) es un max.
Los componentes de la primera fila y columna son los negativos de los elementos de la orla (derivada de la función de restricción)
Multiplicadores de Lagrange: Este método reduce el problema restringido con n-variables a uno con n+k variables, donde k es el número de restricciones de la función original.
Ejemplo
La primera derivada (FOC) para cada variable y el multiplicador (µ) lleva al óptimo de la función F(x,y) y por ende de f(x,y) y g(x,y).
Dada una función f(x,y), sujeta a g(x,y)=c , se elabora una nueva función F(x,y) que cumple:
F(x,y) = f(x,y) - µ (g(x,y) - c)
Sustitución: Asi como su nombre lo detalla, la idea es sustituir variables para simplificar el análisis. De esto modo, se tiende a poner la restricción G(x,y) en función de una variable, para poder sustituir en F(x,y).
Resolviendo Rest. se encuentra:
x = 1
El punto crítico de w es (1,-1,2)
Resolviendo w (con derivadas parciales)
se encuentra:
y = -1 & z = 2
Sustituido: w = (y - 2z + 6)2 + y2 + z2
Ya que: x = y - 2z +6
Dada: w = x2 + y2 + z2
Sujeta a: x - y - 2z = 6
Sin Restricciones
El método más común es la Matriz Hessiana, que se compone de las derivadas parciales de la función. Aunque este compuesta de derivadas, la Hessiana no es una función.
Para un H3, es necesario que:
Max = |H1|<0 ; |H2|>0 ; |H3|<0
Min = |H1|, |H2| y |H3| < 0
Para un H2, es necesario que:
Max = |H1|<0 y |H2|>0
Min = |H1|>0 y |H2|>0
Para encontrar el min o max, se evaluate las derivadas en un punto crítico y después de analizan sus determinantes.
Se utilizan las herramientas de las Derivadas Parciales para desarollar el análisis.
Optimización
multivariable
Segunda Derivada Parcial (SOC multivariable): Puede indicar cómo cambia una variable en función de la otra, si se realiza la derivada parcial cruzada (∂f / ∂x ∂y).
Se puede ver como: ∂2f/∂x2 o, si es cruzada, ∂f/∂y∂x.
Matriz Hessiana: Es una matriz compuesta de las segundas derivadas parciales de f(x,y) y tiende a ser simétrica por el Teorema de Young.
Es lo que se utiliza para determinar min o más en multivariable al evualarse en los puntos determinados.
Hessiana = [ 2x + y 2x
x + 2y 2y ]
Ejemplo: x2 + xy +y2
∂f/∂x = 2x + y
∂f∂y = x + 2y
∂f/∂x∂y = 2x
∂f/∂y∂x = 2y
El Teorema de Young dice que las SOC parciales son iguales, o sea:
∂f / ∂x ∂y = ∂f / ∂y ∂x
Primera Derivada Parcial (FOC multivariable): Se utiliza el mismo procedimiento, solo que se deriva con respecto a una variable mientras que las demás se mantienen constantes.
Se utiliza "∂f/∂x" para indicar respecto a cual variable se deriva.
Ejemplo: f(x,y) = 2x2 + xy +3y2
∂f/∂x = 4x + y
∂f/∂y = x + 6y
Organizando las FOC en un vector columna se encuentra el Vector Gradiente. Esto indica la dirección en la que más rápido cambia de valor la función.
∆f = [ 4x + y
x + 6y ]
Geometricamente representa la tasa de cambio de una variable en un plano perpendicular a la figura que forma la función.
Optimización de
una variable
Condición de Segundo Orden (SOC): Se encuentra al derivar la FOC, o sea haciendo una segunda derivada de f(x) y lo que permite encontrar es si el punto encontrado en FOC es un mínimo, máximo o inflexión.
Si cuando se deriva, queda la variable presente en la función, entonces se evalúa la función en el punto encontrado en FOC.
Si SOC < 0, entonces FOC es un máximo.
Si SOC = 0, entonces FOC es punto de inflexión.
Si SOC > 0, entonces FOC es un mínimo.
Condición de Primer Orden (FOC): Se puede encontrar el valor que maximiza o mínimiza la función. Esto se realiza al igualar la primera derivada a cero.
f(x) = 2x2 -4x +6
f'(x) = 4x -4
f'(x) = 4x -4 = 0
=> x = 1
Esto implica que f(x) tiene un máximo en x=1.
Tanto con una o más variables, se trata de analizar el cambio de una función al generar un cambio en una variable.
Funciones en R
Derivadas e Integrales
Integral: Es el área debajo de una función. Se determina analizando la función y evaluando en su punto inicial y final.
Derivada: Es el ritmo de cambio de una función en un punto determinado. Viene a ser la pendiente de una recta tangente en el punto dado.
Composición
Una función esta compuesta de otra cuando su conjunto de imágenes son parte del dominio de la otra. Es decir que el resultado que es G(F(x) utiliza los resultados de F para producir G.
Continuidad
Una función es continua cuando se puede "dibujar sin levantar el lápiz", o bien, es diferenciadle en cualquier punto.
Función Cuadrática
Forma Lineal:
ax2 +bx +c = 0
A = πr2
Forma Matricial:
[x1 x2] [a11 a12 [x1
0 a22] x2]
Tiene un grado máximo de 2
Función Lineal
Formas en que aparece representada:
Forma Lineal:
Y = mx + b
C = πr
Forma Matricial:
[ a b [ x = [ h
c d ] y ] = g ]
Forma Canónica:
X = [1 [0
x1 0 x2 1
0] 0]
Tiene grado máximo de 1
Álgebra lineal
Otros temas
Ortogonalidad
Dos o más vectores son ortogonales si su producto es 0.
Debe cumplir: vt x w = 0
Geometricamente: Ortogonalidad significa que los vectores son perpendiculares entre ellos mismos.
Bases
Las bases son vectores linealmente independientes que generan la totalidad de vectores en el espacio.
Esto se obtiene al realizar operaciones con ellos mismos. Tanto multiplicación como suma y resta está permitido.
Dependencia líneal
Dos o más vectores son dependientes si los escalares µ1 y µ2 son distintos a 0.
Esto implicaría que V es un múltiplo escalar de W, ya que:
V = -µ2/µ1 x W
Se dice que dos vectores son independientes si se cumple que µ1V + µ2W = 0
Esto quiere decir que µ1 y µ2 tienen que ser escalares nulos, para obtener el vector nulo "0".
Eigenstuff
Diagonilización de matrices: Una matriz diagonalizable es aquella que se puede transformar en una matriz diagonal.
Se descompone en A = PDP-1
Donde: A = matriz a diagonalizar
P = matriz cuyas columnas son los vectores propios
D = matriz diagonal formada por los valores propios
P-1 = inversa de P
Procedimiento para calcular:
1. Calcular la ecuación característica al resolver | A - µ I |
2. Hallar las raices del polinomio característico, los cuales son los valores propios.
3. Calcular los vectores propios usando (A - µI)v = 0
y = -5x => y= 5
V1 = [ 1
5 ]
|A| = µ2 -3µ +2
µ1 = 1
µ2 = 2
µ1 => (A - 1I)v = 0
[0 0 [x = 0
5 1] y] = 0
A = [ 1 0 - µ = [ µ µ x I = [ 1 0
5 2 ] µ µ ] 0 1 ]
A = [ 1-µ 0
5 2-µ ]
|A| = (1-µ)(2-µ)
Si existe una combinación lineal entre filas o columnas, como mínimo un valor propio será 0.
El producto de todos los valores propios de A es igual al valor de su determinante.
La suma de la diagonal principal de A es igual a la suma de sus valores propios.
Un vector propio debe ser distinto de 0, pero un valor propio si puede ser 0.
Un escalar µ es un valor propio de A si existe una solución no trivial de v (solución distinta a 0 de v).
Un vector propio de A es un vector distinto de 0 que cumple Av = µv. Donde A es la matriz, v el vector y µ el valor propio.
Definición: Los vectores propios son vectores no nulos de una aplicación linean (ecuación o matriz) que, cuando son multiplicados o transformados por ella, dan como resultado un múltiplo escalar de ella.
Geométricamente: Son vectores y valores que al multiplicar una matriz o vector por ellos, dan como resultado una línea. Logran transformar una matriz a una línea en el espacio.
Sistemas de ecuaciones
Aplicaciones y Soluciones
Operaciones básicas: Las operaciones aplicables en Sistemas de Ecuaciones y Matrices de coeficientes son...
1. Intercambiar dos filas de una matriz.
2. Cambiar una fila al sumar un multiplo de otra fila.
3. Multiplicar los elementos de una fila por un número distinto de 0.
Método de Gauss-Jordan: Consiste en reducir el sistema al mismo tiempo que se encuentra su inversa. Se utiliza la matriz a reducir y al lado la identidad de mismo orden.
A = [ 2 -3 | 1 0
-4 5 | 0 1 ]
A = [ 1 0 | -5/2 -3/2
0 1 | -2 -1 ]
A-1 = [ -5/2 -3/2
-2 -1 ]
Método de Gauss: Consiste en obtener una matriz de coeficientes que sea triangular, al aplicar operaciones con las ecuaciones (combinaciones lineales). Una vez finalizado, la ultima ecuación tiene una incógnita que se puede resolver y sustituir en las demás ecuaciones.
A = [ 6 -2 -2 [ x1 [ 8
2 2 1 x2 = 3
1 2 2 ] x3 ] -1 ]
Ar = [ 1 2 2 | -1
0 -2 -3 | 5
0 0 7 | -21 ]
7x3 = -21 => x3 = -3
Método de Cramer: La regla de Cramer proporciona los valores de las soluciones siempre y cuando se cumpla:
1. Se trate de un sistema cuadrado, o sea m = n (m ecuaciones y n variables).
2. El determinante de la matriz de coeficientes no es nulo.
Las soluciones se obtienen con: el cociente (división) de determinantes. En el numerador se calcula el determinante resultante de cambiar la i-esima columna por la columna independiente.
X = [ 6 -2 3
2 -1 1 dividido por |A|
1 0 -1 ]
A = [ 1 -2 3 X = [ X B = [ 6
2 -1 1 Y 2
1 0 -1 ] Z ] 1 ]
Aplicaciones: Se pueden resolver muchas cosas utilizando ecuaciones lineales y sistemas sistemas de las mismas.
Teorema de Rouché-Frobenius: Sea AX=B un sistema con m ecuaciones y n variables....
Sistema Compatible: Si los rangos coinciden.
Compatible Indeterminado: Si el rango es menor n.
Compatible Determinado: Si el rango coincide con n.
Sistema Incompatible: Si el rango de la matriz de coeficientes "A" es distinto al rango de la matriz ampliada "A|B".
Soluciones de Sistemas de Ecuaciones: según la cantidad de soluciones, se clasifican de esta manera....
Sistema Incompatible
No tiene solución
Sistema Compatible
Compatible indeterminado: tiene más de una solución.
Compatible determinado: tiene solución única.
Interés principal: Los sistemas de ecuaciones buscan responder la pregunta "¿existe una solución?", de ser positiva, pregunta "¿cuántas soluciones existen?"
Tipos de Sistemas de Ecuaciones
En forma matricial: AX = B
Si hay más de una línea, entonces el resultado se puede interpretar como una matriz.
1. a1x2 + a2x2 ...
2. b1x1 + b2x2 ...
Donde: A= [a1 a2 ... an]
X = [ x1
x2
...
x3
En forma lineal: b = a1x1 + a2x2 + ... + anxn
Una ecuación lineal contiene parámetros y variables.
b = a1x1 + a2x2 + ... + anxn
Donde "a" son parametros y "x" son variables.
Definición: Un sistema de ecuaciones está compuesto por ecuaciones lineales. Ecuación lineal es aquella que su grado más alto es 1. La famosa y=mx+b.
Determinantes
Aplicaciones
Encontrar la inversa de una matriz: el determinante se utiliza para encontrar los cofactores, la matriz adjunta y la inversa de la matriz.
Matriz inversa: Está definida en Matrices - Tipos de Matrices.
Se calcula usando el determinante y la adjunta traspuesta.
A-1 = 1/|A| x Adjt
Matriz adjunta: Es una matriz formada por sus cofactores multiplicados por (-1)i+j. Esto significa que los adjuntos pueden cambiar de signo.
Adj = [C11 C12 C13
C21 C22 C23
C31 C32 C33]
Cofactor de un elemento (Menor complementario): Es el determinante de la matriz que se obtiene al "suprimir" la fila y la columna del elemento en cuestión.
Multiplicando los cofactores de una fila o columna de A, se obtiene el determinante de una matriz de orden 3x3 o más grande. Se conoce también como Expansión de Cofactores.
C11 = [ a22 a23
a32 a33 ]
Geometricamente (en un plano de vectores) el determinante representa el área entre los mismos. Se hace un paralelogramo (especie de cuadrado) con los vectores y ese espacio es el determinante.
Representación
El determinante de un producto es igual al producto de los determinantes.
|AB| = |A| x |B|
Si todos los elementos de una fila o columna están formadas por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás filas o columnas permaneces iguales.
|A| = [ a11+b11 a12+b12 a13+b13
a21 a22 a23
a31 a32 a33 ]
|A| = [a11 a12 a13 |B| = [b11 b12 b13
a21 a22 a23 + a21 a22 a23
a31 a32 a33 ] a31 a32 a33 ]
Si a los elementos de una fila o columna se le suman (o restan) los elementos de otra, no el determinante no cambia.
Si en una matriz se cambian dos filas o columnas entre sí, su determinante cambia de signo.
Ao = [a11 a12 a13
a21 a22 a23
a31 a32 a33]
|A| = A
Am = [a11 a13 a12
a21 a23 a22
a31 a33 a32]
|A| = -A
El determinante de una matriz triangular es igual al producto de los elementos de su diagonal principal.
A = [a11 a12 a13
0 a22 a23
0 0 a33]
|A| = a11 x a22 x a33
El determinante es 0 cuando:
Los elementos de una fila o columna son una combinación de otra.
A = [ X Y Z
2X 2Y 2Z
E. F G ]
Todos los elementos de una fila o columna son nulos.
A = [ 0 0 0
X Y Z
E F G ]
La matriz tiene dos filas o columnas iguales.
A = [ X Y Z
X Y Z
E F G ]
El determinante de una matriz y su traspuesta son iguales.
Algebraicamente: |A| = |At|
Se denota como |A|
Definición: Es una función que tiene de entrada una matriz cuadrada y como salida un número real.
Matrices
Tipos de matrices
Matriz regular: Aquella que admite inversa porque su determinante es diferente a cero.
Matriz singular o única es la que no tiene inversa, porque su determinante es igual a 0.
Matriz ortogonal: Es una matriz que multiplicada por su traspuesta da como resultado la identidad.
Su traspuesta es igual a la inversa ( At = A-1 )
Matriz inversa: Es una matriz que multiplicada por la original, da como resultado la matriz identidad.
Si la matriz existe entonces se llama regular, si no existe, se llama única.
Siendo entonces: A x A-1 = I
También cumple: A-1 x A = I
Matriz ídempotente: Es una matriz que multiplicada por ella misma, da como resultado ella misma.
Siendo entonces: A x A = A
Matriz simétrica: Es una matriz cuya traspuesta es igual a ella misma.
La Matriz antisimetrica es la que su traspuesta es igual a la opuesta. Entonces: At = -A
Siendo entonces: a12 = a21, a13 =a31, etc.
Matriz traspuesta: Es una matriz cuyas columnas y filas han sido cambiadas. Se denota como A^t
At = [a11 a21 a31
a12 a22 a32
a13 a23 a33]
Matriz idéntica o igual: Es una matriz cuyos elementos son iguales a los de otra, además su orden es igual,
Matriz identidad: Es una matriz diagonal que tiene “1” en sus componentes. Se denota como I
A = [ 1 0 0
0 1 0
0 0 1]
Matriz diagonal: Es una matriz que solo tiene elementos en su diagonal principal.
A = [a11 0 0
0 a22 0
0 0 a33]
Matriz triangular: Son matrices que tienen solo tienen elementos arriba o abajo de la diagonal principal, incluyendo los de la diagonal.
Triangular inferior: Elementos por debajo de la diagonal princípial.
A = [a11 0 0
a21 a22 0
a31 a32 a33]
Triangular superior: Elementos por encima de la diagonal principal.
A = [a11 a12 a13
0 a22 a23
0 0 a33]
Matriz cuadrada: Es una matriz que tiene la misma cantidad de filas y columnas. Su orden es “n x n”
Tiene una Diagional Principal, que está conformada por los elementos de igual subíndice. O sea, a11 a22 ... ann
A = [a11 a12 a13
a21 a22 a23
a31 a32 a33]
Matriz opuesta: Es una matriz similar a A, pero que sus elementos están multiplicados por -1.
A = [1 2 3]
-A = [-1 -2 -3]
Matriz nula: Es aquella culyos elementos son nulos, o sea 0.
A=[0 0 0]
Matriz columna: Matriz conformada por una sola columna de números. También conocida como “vector columna”.
C=[a11
a21
...
an1]
Matriz fila: Matriz conformada por una sola fila de números. También conocida como “vector fila”.
F=[a11 a12 ... a1n]
Propiedades
Rango: Número máximo de filas o columnas que son linealmente independientes. (No dependen o son una combinación de ellas mismas.)
Geometricamente: Significa que al graficar los vectores, no están en la misma línea. De tener direcciones diferentes se dice que son independientes.
Si se observa que son paralelas entonces se cumple que son una combinación lineal de si mismas.
Representación: Los componentes de A (matriz) son “a” y tienen subíndices “i” para filas y “j” para columnas.
A=[aij]
Orden: Número de filas por el número de columnas. Se representa como “m x n”, donde “m” es filas y “n” es columnas.
Definición: Conjunto de números dispuestos en filas y columnas.