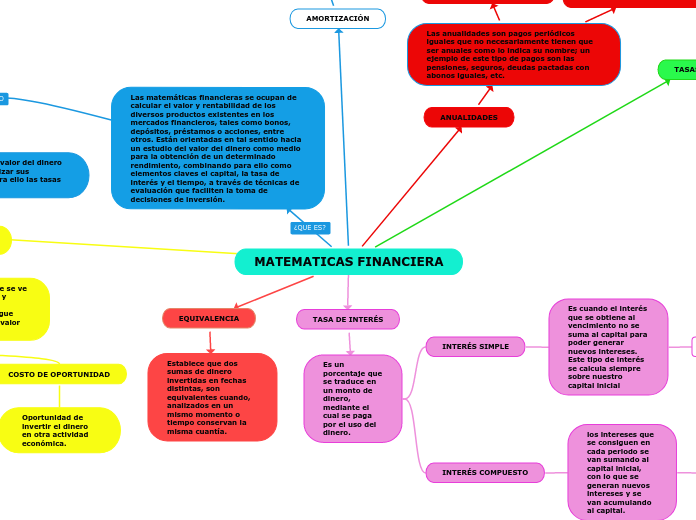
MATEMATICAS FINANCIERA
AMORTIZACIÓN
Es el proceso mediante el cual se distribuyen gradualmente los costos de una deuda por medio de pagos periódicos. Los pagos o cuotas servirán para pagar los intereses de tu crédito y reducir el importe de tu deuda.
ANUALIDADES
Las anualidades son pagos periódicos iguales que no necesariamente tienen que ser anuales como lo indica su nombre; un ejemplo de este tipo de pagos son las pensiones, seguros, deudas pactadas con abonos iguales, etc.
ANUALIDADES VENCIDAS
Es aquella en que los pagos se efectúan al final del periodo.
ANUALIDADES ANTICIPADAS
Es aquella en que los pagos se efectúan al principio del periodo o mes.
TASAS
TASA ANTICIPADA
Cuando el interés se causa en forma anticipada en el período. Cabe anotar que la Tasa Efectiva no puede darse, por definición, en forma anticipada, es decir no existe una tasa efectiva anticipada.
TASA EFECTIVA ANUAL EA
Es el interés que debes pagar al año por utilizar ese dinero.
Tipos de tasa efectiva anual
TASA EFECTIVA ANUAL VARIABLE
pueden fluctuar a su favor o en su contra. Entonces, si bien una tasa efectiva anual variable podría ofrecer tasas de interés más bajas inicialmente, también puede aumentar a medida que aumenta el índice al que está vinculada, lo cual es una desventaja de las tasas efectivas anuales variables. A menudo encontrará este tipo de tasa efectiva anual en tarjetas de crédito (en inglés).
TASA EFECTIVA ANUAL FIJA
Quiere decir que no cambia según un índice durante la vigencia del préstamo. Debido a esto, las tasas efectivas anuales fijas pueden ser más predecibles a la hora de presupuestar. Algunos ejemplos comunes de préstamos con tasas efectivas anuales fijas incluyen la mayoría de las hipotecas y préstamos personales.
TASA NOMINAL
La tasa de interés nominal es aquella que se paga por un préstamo o una cuenta de ahorros y no se suma al capital, es expresada en términos anuales con una frecuencia de tiempo de pago, por ejemplo: Tasa nominal anual del 10% pagadera mes vencido. Se asimila a la tasa de interés simple.
TASA PERIÓDICA
La tasa corresponde al período de composición (% por día, mes, bimestre, trimestre, semestre, año, etc.). Algunos sectores la conocen como tasa efectiva periódica (efectiva diaria, efectiva mensual, efectiva trimestral, etc.),
TASA DE INTERÉS
Es un porcentaje que se traduce en un monto de dinero, mediante el cual se paga por el uso del dinero.
INTERÉS COMPUESTO
los intereses que se consiguen en cada periodo se van sumando al capital inicial, con lo que se generan nuevos intereses y se van acumulando al capital.
Caracteristicas
° El capital inicial aumenta en cada periodo debido a que los intereses se van sumando.
° La tasa de interés se aplica sobre un capital que va variando.
° Los intereses son cada vez mayores.
VA = VF (1 + i) ^n
VF = Valor Futuro
VA = Valor Actual
i = Tasa de interés
n = Periodo de tiempo
INTERÉS SIMPLE
Es cuando el interés que se obtiene al vencimiento no se suma al capital para poder generar nuevos intereses. Este tipo de interés se calcula siempre sobre nuestro capital inicial
Características
° El capital inicial se mantiene igual durante toda la operación.
° El interés es el mismo para cada uno de los períodos de la operación.
° La tasa de interés se aplica sobre el capital invertido o capital inicial.
Formula
VF = VA (1 + n * i)
VF = Valor Futuro
VA = Valor Actual
i = Tasa de interés
n = Periodo de tiempo
Podemos obtener el interés que produce un capital con la siguiente fórmula:
I = C * i * n
EQUIVALENCIA
Establece que dos sumas de dinero invertidas en fechas distintas, son equivalentes cuando, analizados en un mismo momento o tiempo conservan la misma cuantía.
EL VALOR DEL DINERO EN EL TIEMPO
Es el reflejo del poder adquisitivo que se ve afectado por fenómenos económicos y financieros que podrían aumentar o disminuir el valor, y cuando se consigue igualdad entre el valor presente y el valor futuro.
COSTO DE OPORTUNIDAD
Oportunidad de invertir el dinero en otra actividad económica.
RIESGO
La probabilidad de perdida del dinero y no poderlo recuperar.
INFLACIÓN
Cuando los bienes y servicios aumentan su precio de forma general y constante, reduciendo así, el valor del dinero.
Las matemáticas financieras se ocupan de calcular el valor y rentabilidad de los diversos productos existentes en los mercados financieros, tales como bonos, depósitos, préstamos o acciones, entre otros. Están orientadas en tal sentido hacia un estudio del valor del dinero como medio para la obtención de un determinado rendimiento, combinando para ello como elementos claves el capital, la tasa de interés y el tiempo, a través de técnicas de evaluación que faciliten la toma de decisiones de inversión.
determinar la evolución del valor del dinero en relación al tiempo y analizar sus implicaciones, utilizando para ello las tasas de interés.