Modelos de Optimización
Web grafía
Ramos, A., Sanchez, P., Ferrer, J., Barquín, J., Linares, P., 2010
Modelos matemáticos de optimización
Universidad Pontifica Comillas Madrid, Pag. 4 -5
http://www.gams.com/docs/contributed/modelado_en_gams.pdf
Munguia, L., Protti., M., 1998
Investigación de Operaciones
Editorial EUNED, Pag. 5
Google Scholar
https://books.google.fr/books?id=6NHEmmbHGcoC&pg=PA424&dq=Taha,++H.A.++%281998%29
Carmona, F., 2005
Universidad de Barcelona
http://dialnet.unirioja.es/servlet/libro?codigo=255789
Universidad Autónoma del estado de Hidalgo, 2011
Tipos de Modelos de Investigación de Operaciones
http://www.uaeh.edu.mx/docencia/P_Presentaciones/huejutla/sistemas/investigacion_operaciones/modelos.pdf
Taha, Hamdy. A., 2012
Investigación de Operaciones, Novena edición, Pag. 37-44
https://jrvargas.files.wordpress.com/2009/01/investigacic3b3n-de-operaciones-9na-edicic3b3n-hamdy-a-taha-fl.pdf
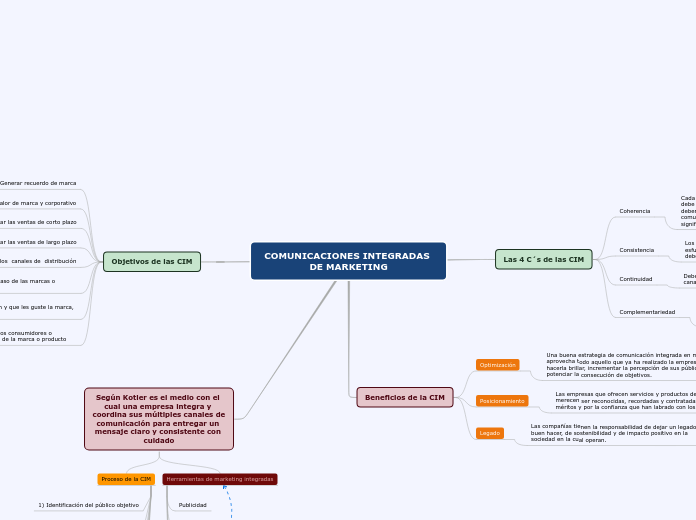
Clasificación
Modelos Determinísticos y Estocásticos
Los modelos que se basan en las probabilidades y estadísticas y que se ocupan de incertidumbres futuras se llaman probabilísticos o estocásticos.
Los modelos que no tienen consideraciones probabilísticas se llaman determinísticos, el PERT, los inventarios y la programación lineal, enfocan su atención en aquellas circunstancias que son criticas y en los que las cantidades son determinadas y exactas.
Modelos enteros y no enteros
Los modelos que no se prestan para usar datos empíricos o simulados en forma aleatoria y fraccionaria son modelos no enteros.
En un modelo de simulación los datos de entrada pueden ser reales o generados en forma aleatoria, pero las variables deben ser enteros. En el PC se puede preparar un modelo entero simulado paso por paso donde se puede reproducir el funcionamiento de sistemas o problemas de gran escala.
Modelos Estáticos y Dinámicos
Un modelo dinámico por el contrario está sujeto al factor tiempo que desempeña un papel esencial en la secuencia de las decisiones, independientemente de cuáles hayan sido las decisiones anteriores. A la programación dinámica pertenecen estos modelos.
Los modelos estáticos se ocupan de determinar una respuesta para una serie especial de condiciones fijas que probablemente no cambiaran significativamente a corto plazo, es decir, la solución está basada en una condición estática.
Modelos Lineales y no lineales
Un modelo no lineal es aquel donde las variables de decisión se expresan como funciones no lineales ya sea en la función objetivo y/o restricciones de un modelo de optimización. Esta característica particular de los modelos no lineales permite abordar problemas donde existen economías o deseconomías de escala o en general donde los supuestos asociados a la proporcionalidad no se cumplen.
Los modelos lineales constituyen una de las metodologías estadísticas más ampliamente utilizadas en la modelización y el análisis de datos de todo tipo. Se introducen en campos tan diversos como la experimentación industrial, la construcción y validación de test psicológicos o el análisis de datos.
Los modelos de optimización pueden representar diferentes tipos de situaciones que manifiestan un comportamiento lineal, no lineal, estático o dinámico, entre otros.
Partes
Restricciones
Representan el conjunto de relaciones (expresadas mediante ecuaciones e inecuaciones) que ciertas variables están obligadas a satisfacer.
o Capacidad de producción
o Dimensiones del material
o Número máximo de inventarios
o Máxima cantidad de inversión
Variables de decisión
Son las decisiones que se pueden tomar para afectar el valor de la función objetivo. Pueden ser independientes o dependientes.
o cantidad de productos en inventario
o cantidad de empleados
o cantidad de producto que se fabrica
Función objetivo
Es la medida cuantitativa máxima o mínima del funcionamiento del sistema que se desea optimizar
o Minimización de costos de operación
o Maximización de beneficios netos por ventas
o Minimización del material utilizado en la fabricación
En que consiste?
Sin embargo los resultados obtenidos, desde el punto de vista matemático no siempre pueden ser tomados literalmente, ya que existen muchos factores intangibles que afectan las decisiones y deben ser considerados en la toma de decisiones finales.
Resolver un problema de optimización consiste en encontrar el valor que deben tomar las variables para hacer óptima la función objetivo satisfaciendo el conjunto de restricciones.
Elementos
Son elementos del sistema (empresa, comunidad, sociedad, entre otros) se relacionan y se comportan de manera inesperada.
Que es?
Modelo
Esquema teórico, generalmente en forma matemática, de un sistema o de una realidad compleja, que se elabora para facilitar su comprensión y el estudio de su comportamiento
Optimización
Es encontrar una alternativa de decisión con la propiedad de ser mejor que cualquier otra en algún sentido.
Técnicas
En la investigación de operaciones no se cuenta con una técnica general única para resolver todos los modelos que puedan surgir en la práctica. En su lugar, el tipo y complejidad del modelo matemático determina la naturaleza del método de solución.
Historia
Las primeras actividades formales de investigación de operaciones (IO) se iniciaron en Inglaterra durante la Segunda Guerra Mundial, cuando un equipo de científicos empezó a tomar decisiones con respecto a la mejor utilización del material bélico. Al término de la guerra, las ideas formuladas en operaciones militares se adaptaron para mejorar la eficiencia y productividad en el sector civil.