von Sebastian Ortiz Vor 5 Jahren
3378
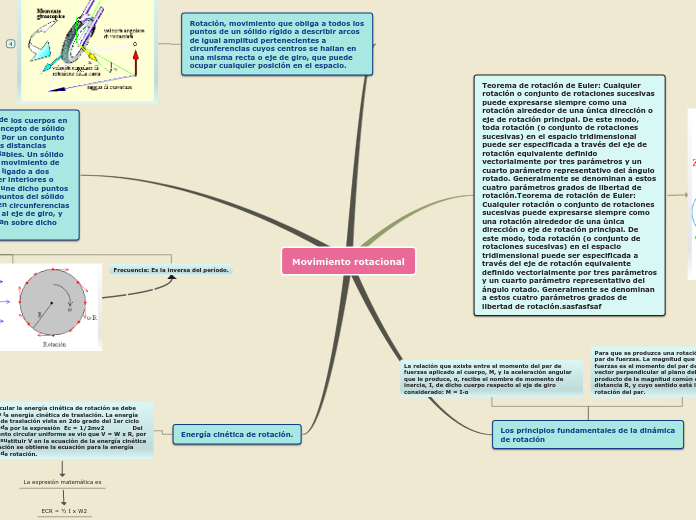
Movimiento rotacional
La energía cinética de rotación se calcula a partir de la energía cinética de traslación, utilizando la ecuación Ec = 1/2mv^2 y sustituyendo la velocidad V por el producto de la velocidad angular W y el radio R.