Sets & Whole-Number Operations and Properties
The goal of this map is to outline everything you need to learn about sets and whole-number operations and properties for Kindergarten through 6th grade.
Division of Whole Numbers
As with multiplication, division of whole numbers would have the closure property provided that when we divide two whole numbers, the quotient is a unique whole number.
In the division of whole numbers a and b, b does not equal 0, a/b=c if and only if c is a unique whole number such that c x b=a. In the equation, a/b=c, a is the dividend, b is the divisor, and c is the quotient.
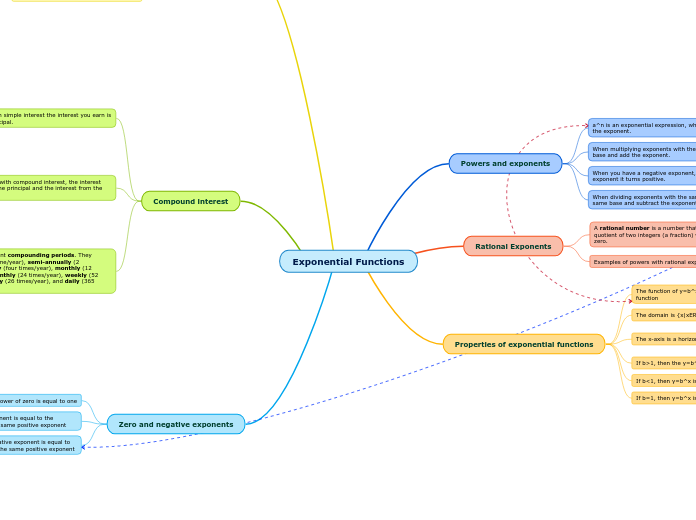
Sets & Whole Numbers
Whole Numbers
Whole number=the unique characteristic embodied in each finite set and all the sets equivalent to itCardinality=the number of elements in set A is expressed as n(A)Less than is symbolized as <Greater than is symbolized as >Set of natural numbers=infinite set, proper subset of whole numbers, also called the set of counting numbers, does not include 0Set of even numbers=a proper subset of the set of whole numbers starting with 0 and continuing with every second number after thatSet of odd numbers=proper subset of the whole numbers that remains after the even numbers are removedSets
Set=any collection of objects or ideas that can be listed or describedElement=each individual object in a setOne-to-one correspondence=Sets A & B have one-to-one correspondence if and only if each element of A is paired with exactly one element of B and each element of B is paired with exactly one element of AEqual sets=Sets A & B are equal sets if and only if each element of A is also an element of B and each element of B is also an element of A (symbolized A=B)Equivelent sets=Sets A & B are equivalent sets if and only if there is a one-to-one correspondence between A and B (symbolized by A ~ B)Subset=For all sets A & B, A is a subset of B if and only if each element of A is also an element of B (symbolized as A C B)Proper Subset=For all sets A & B, A is a proper subset of B if and only if A is a subset of B and there is at least one element of B that is not an element of A (symbolized as A C B)Complement=The complement of set A consists of all of the elements in U that are not in AUnion of 2 sets=A and B is the set containing every element belonging to set A or set B and is written A U BIntersection of 2 sets=A and B is the set containing every element belonging to both set A and set BDisjoint sets=if and only if their intersection is the empty setMultiplication of Whole Numbers
Closure property of multiplication=for whole number a and b, a x b is a unique whole numberIdentity property of multiplication=there exists a unique whole number, 1, such that 1 x a = a x 1 = a for every whole number a. Thus 1 is the multiplicative identity elementCommutative property of multiplication=for whole number a and b, a x b = b x aAssociative property of multiplication=for whole numbers a, b, and c, (a x b) x c = a x (b x c)Zero property of multiplication=for each whole number a, a x 0=0 x a=0Distributive property of multiplication over addition=for whole numbers a, b, and c, a x (b+c)=(a x b) + (a x c)Distributive Property of Multiplication
Distributive property of multiplication over addition=for whole numbers a, b, and c, a x (b+c)=(a x b) + (a x c)
Zero Property of Multiplication
Zero property of multiplication=for each whole number a, a x 0=0 x a=0
Associative Property of Multiplication
Associative property of multiplication=for whole numbers a, b, and c, (a x b) x c = a x (b x c)
Commutative Property of Multiplication
Commutative property of multiplication=for whole number a and b, a x b = b x a
Identity Property of Multiplication
Identity property of multiplication=there exists a unique whole number, 1, such that 1 x a = a x 1 = a for every whole number a. Thus 1 is the multiplicative identity element
Closure Property of Multiplication
Closure property of multiplication=for whole number a and b, a x b is a unique whole number
Multiplication as repeated addition=if there are m sets with n objects in each set, then the total number of objects (n+n+n+...+n, where n is used as an addend m times) can be represented by m x n, where m and n are factors and m x n is the productMultiplication of whole numbers=if A and B are finite sets with a = n(A) and b = n(B), then a x b = n(A x B). In the equation a x b = n(A x B), a and b are called factors and n(A x B) is called the productSubtraction of Whole Numbers
Even though subtraction of whole numbers is closely related to addition of whole numbers, the properties of addition do not hold for subtraction.
In the subtraction of the whole numbers a and b, a-b=c if and only if c is a unique whole number such that c+b=a. In the equation a-b=c, a is the minuend, b is the subtrahend, and c is the difference.
Addition of Whole Numbers
Properties
Closure property of addition=for whole numbers a and b, a+b is a unique whole numberIdentity property of addtion=there exists a unique whole number, 0, such that 0+a=a+0 for every whole number a. Zero is the additive identity element.Commutative property of addition=for whole number a and b, a+b=b+aAssociative property of addition=for whole numbers a,b, and c, (a+b)+c=a+(b+c)Associative Property of Addition
Associative property of addition=for whole numbers a,b, and c, (a+b)+c=a+(b+c)
Commutative Property of Addition
Commutative property of addition=for whole number a and b, a+b=b+a
Identity Property of Addition
Identity property of addtion=there exists a unique whole number, 0, such that 0+a=a+0 for every whole number a. Zero is the additive identity element.
Closure Property of Addition
Closure property of addition=for whole numbers a and b, a+b is a unique whole number
Definitions
In the addition of whole numbers, if A and B are two disjoint sets, and n(A) = a and n(B) = b, then a+b=n(AUB).
In the equation a+b=c, a and b are addends and c is the sum