Integer Uses
Golf Scores
Check out this video that explains how golf scores use integers.
Money
When working with money, be it cash, checking or credit card. You can look at the money you spent, a negative sum and the money you earned as a positive sum. In the instance of a checkbook, you need to balance, hopefully keeping your account in the positive.
Adding Integers using Money Analogy
Stock Gain/Loss
Check out this video for every day uses of Integers, using the example of stocks, losses and gains.
Altitude
Geographically, we represent sea level with integers. Obviously, below sea level is represented with negative integers.
Temperature
When reading a thermometer you read above zero temperatures as positive and below zero temperatures as negative.
Understanding integers using temperature
Sources: All videos and links are linked to source of origin. Further information is courtesy of O'Daffer, Charles, Cooney, Dossey, and Schielack
What are Integers?
Integers consist of positive integers, negative integers, and zero.
An integer is a whole number that can be either greater than 0, called positive, or less than 0, called negative. Zero is neither positive nor negative.
Two integers that are the same distance from zero in opposite directions are called opposites.
Every integer on the number line has an absolute value, which is its distance from zero.
Check out Math.com for more in depth definition, examples, and a workout.
Integers are like whole numbers, 0, 1, 2,3,4,5 ..., but they also include negative numbers. integers can be negative {-1, -2,-3, -4, -5, … }, positive {1, 2, 3, 4, 5, … }, or zero {0}
Subtopic
Integers 101
Outlined in this map is basic information that you need to know about integers, weather you are a student, teacher or parent.
Use this map to learn about integers and look back to this map as a future tool or guide when you are working with integers. There are many attachments that allow you to see video demonstrations but practice sites as well.
As a parent or teacher please use this site as a refresher. We have all been there where you remember but don’t quite remember. Also, a lot has changed over time, so I’ve attached the most up-to-date information and examples.
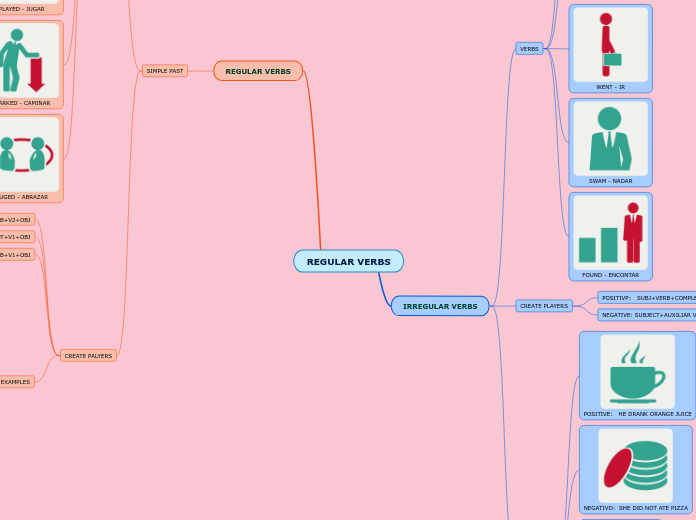
Multiplication, Division, and Other Properties of Integers
Integer Division
Procedures for Dividing Integers
Dividing two positive integers: Divide as with whole numbers.
Dividing with two negative integers: Divide absolute values. The quotient is positive.
Dividing a positive and a negative integer: Divide absolute values. The quotient is negative.
Dividing by an integer can be thought of as finding the missing factor.
Eampled
28/ 4 = ?
Think: What number multiplied by 4 gives the product 28?
28/4=7
This process works for all integers.
Check out this video with Integer Division
Procedures for Multiplying Integers
Multiplying two positive integers: Multiply as with whole numbers.
Multiplying two negative integers: Multiply absolute values, the product is positive.
Multiplying a positive and a negative integer: Multiply absolute values. The product is negative.
First factors, positive integers, they are modeled by walking east, negative integers by walking west.
In the second factor, positive integers are modeled by hours from now, negative integers by hours ago.
In the product, positive integers are modeled by miles east of zero, negative integers by miles west of zero.
Check out this example of Number-Line Model Multiplication
Charged-Fields Model
A positive number is modeled by putting positive charges into the field and a negative number is modeled by putting in negative charges into the field.
It is modeled by putting multiples of same-size groups of charges when multiplying by a positive integer and taking out multiples of same-size groups of charges when multiplying by a negative integer. The product is the charge of the resulting field.
Example of Charged-Field Model Multiplication
This example is following the equation of
2 x -4 = -8
Use black counters for positive (+) integers and red counters for negative (-) integers.
Use a bag or another devices to represent number of times putting in + or taking out - integers.
See attached picture for example.
Counters Model of Multiplication Examples
Modeling Integer Addition and Subtraction
Procedures for Adding Integers
Adding a positive and a negative integer: Subtract the lesser of the absolute values of the integers from the greater. Give the answer the same sign as the integer with greater absolute value
Adding two negative integers: Add absolute values the sum is negative.
Adding two positive integers: Add as with whole numbers
Modeling Integer Subtraction
As when modeling addition, a person always starts on the number line at 0 and walks on the number line. To model integer subtraction always walk backward after seeing the subtraction sign (-).
Just as addition, a positive number is modeled by putting positive charges into the field a negative number is modeled by putting negative charges into the field.
Subtraction is modeled by putting integral numbers of charges in the field, followed by taking an integral number of charges from the field.
Eample of Charged-Field Model
A counters model may be used to find the differnce of two integers
Recall that because a black and a red counter cancel each other, you can include as many black-red pairs as you want when representing an integer without changing its value.
Counters Model Subtraction
Modeling Integer Addition
Number-Line Model
To represent addition (+), always walk forward and you face right before walking. For negative integers, face left before walking.
Example:
-6 + 4
You draw a number-line picture, you face left, walk 6 followed by face right, walk 4, ending at -2.
In the number-line model a person always starts at zero and "walks" on the number line.
Video depicting Number-Line Model
Charged-Field Model
Example of Charged-Field Model
Based on the idea that the same number of positive and negative charges produces a field with 0 charge, but an excess of positive charges or negative charges produces a result of an negative or positive charged field.
Similar to the counter-model, is the changed-field model
Counters Model
In this example the red counters are used as the model for -3 and the green counters are used for +2.
The sea of zeros is when two chids cancel each other out, or are known as zero. The left over chips that don't zero out represent the answer.
2+ (-3) = -1, since thre is one red chip left.
With counters model one color represents the negative integer, i.e., -1, and another color is used to represent the positive integer, i.e., +1 or 1.
Counters Model Example
Integer Addition Using Counters
Check out this video to see an example of using counters for integer addition. This is an extension of a lesson that this gentleman taught his class, but it does a good job of showing how counters work, even without the original in class lesson.
Absolute Value
Check out this website for and example on how to solve absolute value equations.
The absolute value of a number is positive please keep this in mind.
Ex.
l-6l - l6l = 6 - 6 = 0
First you find the absolute value of l-6l, which is 6, and l6l which is also six. Than you subtract the numbers ending up with zero.
The absolute value of an integer is always positive
no matter if the sign of the integer is negative or positive.
Example:
I 4 I = 4
I -4 I = 4
Remember the absolute value is always the number of units an integer is from zero.
Absolute value of an integer is the number of units the integer is from 0 on the number line.