por Глушонков Илья hace 4 años
560
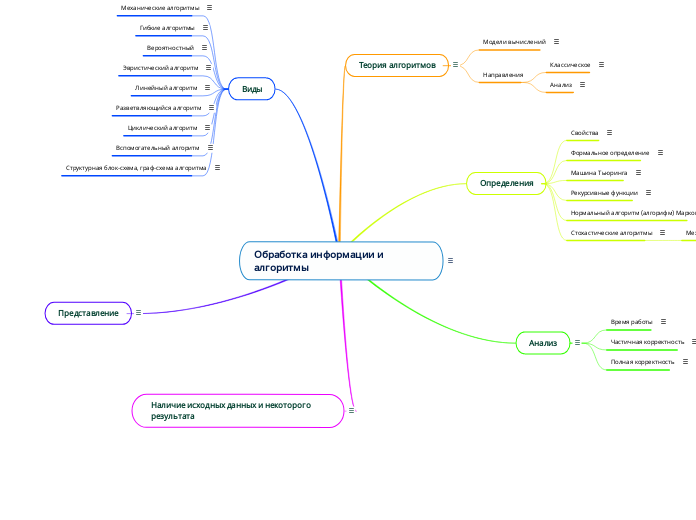
Обработка информации и алгоритмы
por Глушонков Илья hace 4 años
560

Ver más
Алгори́тм (лат. algorithmi — от имени среднеазиатского математика Аль-Хорезми) — конечная совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.
Алгоритм — это точно определённая инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так, алгоритм сложения применим к любой паре натуральных чисел. В этом выражается его свойство массовости, то есть возможности применять многократно один и тот же алгоритм для любой задачи одного класса.
Для разработки алгоритмов и программ используется алгоритмизация — процесс систематического составления алгоритмов для решения поставленных прикладных задач. Алгоритмизация считается обязательным этапом в процессе разработки программ и решении задач на ЭВМ. Именно для прикладных алгоритмов и программ принципиально важны детерминированность, результативность и массовость, а также правильность результатов решения поставленных задач.
Алгоритм — это понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение цели.
Структурная блок-схема, граф-схема алгоритма — графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков — графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия. Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, так как зрительное восприятие обычно облегчает процесс написания программы, её корректировки при возможных ошибках, осмысливание процесса обработки информации. Можно встретить даже такое утверждение: «Внешне алгоритм представляет собой схему — набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации».
Вспомогательный (подчинённый) алгоритм (процедура) — алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм. На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.
Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций). К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно.
Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого может осуществляться разделение на несколько альтернативных ветвей алгоритма.
Линейный алгоритм — набор команд (указаний), выполняемых последовательно во времени друг за другом.
Вероятностный (стохастический) алгоритм даёт программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.
Гибкие алгоритмы, например, стохастические, то есть вероятностные и эвристические.
Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т. п.) — задают определённые действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.
Вместе с распространением информационных технологий увеличился риск программных сбоев. Одним из способов избежания ошибок в алгоритмах и их реализациях служат доказательства корректности систем математическими средствами.
Использование математического аппарата для анализа алгоритмов и их реализаций называют формальными методами. Формальные методы предусматривают применение формальных спецификаций и, обычно, набора инструментов для синтаксического анализа и доказательства свойств спецификаций. Абстрагирование от деталей реализации позволяет установить свойства системы независимо от её реализации. Кроме того, точность и однозначность математических утверждений позволяет избежать многозначности и неточности естественных языков.
Полная корректность — программа завершает работу и выдаёт правильный результат для всех элементов из диапазона входных данных.
Частичная корректность — программа даёт правильный результат для тех случаев, когда она завершается.
Распространённым критерием оценки алгоритмов является время работы и порядок роста продолжительности работы в зависимости от объёма входных данных.[25]
Для каждой конкретной задачи составляют некоторое число, которое называют её размером. Например, размером задачи вычисления произведения матриц может быть наибольший размер матриц-множителей, для задач на графах размером может быть количество ребер графа.
Однако приведённое выше формальное определение алгоритма в некоторых случаях может быть слишком строгим. Иногда возникает потребность в использовании случайных величин[12]. Алгоритм, работа которого определяется не только исходными данными, но и значениями, полученными из генератора случайных чисел, называют стохастическим (или рандомизированным, от англ. randomized algorithm)[13]. Стохастические алгоритмы часто бывают эффективнее детерминированных, а в отдельных случаях — единственным способом решить задачу[12].
На практике вместо генератора случайных чисел используют генератор псевдослучайных чисел.
Однако следует отличать стохастические алгоритмы и методы, которые дают с высокой вероятностью правильный результат. В отличие от метода, алгоритм даёт корректные результаты даже после продолжительной работы.
Некоторые исследователи допускают возможность того, что стохастический алгоритм даст с некоторой заранее известной вероятностью неправильный результат. Тогда стохастические алгоритмы можно разделить на два типа[14]:
Нормальный алгоритм (алгорифм в авторском написании) Маркова — это система последовательных применений подстановок, которые реализуют определённые процедуры получения новых слов из базовых, построенных из символов некоторого алфавита. Как и машина Тьюринга, нормальные алгоритмы не выполняют самих вычислений: они лишь выполняют преобразование слов путём замены букв по заданным правилам[10].
Нормально вычислимой называют функцию, которую можно реализовать нормальным алгоритмом. То есть алгоритмом, который каждое слово из множества допустимых данных функции превращает в её начальные значения[11]..
Создатель теории нормальных алгоритмов А. А. Марков выдвинул гипотезу, которая получила название принцип нормализации Маркова:
Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует некоторый алгоритм, когда функция нормально исчисляемая.
Подобно тезисам Тьюринга и Черча, принцип нормализации Маркова не может быть доказан математическими средствами.
С каждым алгоритмом можно сопоставить функцию, которую он вычисляет. Однако возникает вопрос, можно ли произвольной функции сопоставить машину Тьюринга, а если нет, то для каких функций существует алгоритм? Исследования этих вопросов привели к созданию в 1930-х годах теории рекурсивных функций[9].
Класс вычислимых функций был записан в образ, напоминающий построение некоторой аксиоматической теории на базе системы аксиом. Сначала были выбраны простейшие функции, вычисление которых очевидно. Затем были сформулированы правила (операторы) построения новых функций на основе уже существующих. Необходимый класс функций состоит из всех функций, которые можно получить из простейших применением операторов.
Подобно тезису Тьюринга в теории вычислимых функций была выдвинута гипотеза, которая называется тезис Чёрча:
Числовая функция тогда и только тогда алгоритмически исчисляется, когда она частично рекурсивна.
Доказательство того, что класс вычислимых функций совпадает с исчисляемыми по Тьюрингу, происходит в два шага: сначала доказывают вычисление простейших функций на машине Тьюринга, а затем — вычисление функций, полученных в результате применения операторов.
Таким образом, неформально алгоритм можно определить как четкую систему инструкций, определяющих дискретный детерминированный процесс, который ведёт от начальных данных (на входе) к искомому результату (на выходе), если он существует, за конечное число шагов; если искомого результата не существует, алгоритм или никогда не завершает работу, либо заходит в тупик.
Основная идея, лежащая в основе машины Тьюринга, очень проста. Машина Тьюринга — это абстрактная машина (автомат), работающая с лентой отдельных ячеек, в которых записаны символы. Машина также имеет головку для записи и чтения символов из ячеек, которая может двигаться вдоль ленты. На каждом шаге машина считывает символ из ячейки, на которую указывает головка, и, на основе считанного символа и внутреннего состояния, делает следующий шаг. При этом машина может изменить своё состояние, записать другой символ в ячейку или передвинуть головку на одну ячейку вправо или влево.[8]
На основе исследования этих машин был выдвинут тезис Тьюринга (основная гипотеза алгоритмов):
Некоторый алгоритм для нахождения значений функции, заданной в некотором алфавите, существует тогда и только тогда, когда функция исчисляется по Тьюрингу, то есть когда её можно вычислить на машине Тьюринга.
Этот тезис является аксиомой, постулатом, и не может быть доказан математическими методами, поскольку алгоритм не является точным математическим понятием.
Разнообразные теоретические проблемы математики и ускорение развития физики и техники поставили на повестку дня точное определение понятия алгоритма.
Первые попытки уточнения понятия алгоритма и его исследования осуществляли в первой половине XX века Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Чёрч. Было разработано несколько определений понятия алгоритма, но впоследствии было выяснено, что все они определяют одно и то же понятие (см. Тезис Чёрча — Тьюринга)[6]
Российский математик, основоположник структурной лингвистики в Советском Союзе В. А. Успенский считал, что понятие алгоритма впервые появилось у Эмиля Бореля в 1912 году, в статье об определённом интеграле. Там он написал о «вычислениях, которые можно реально осуществить», подчеркивая при этом: «Я намеренно оставляю в стороне большую или меньшую практическую деятельность; суть здесь та, что каждая из этих операций осуществима в конечное время при помощи достоверного и недвусмысленного метода»[7].
Тео́рия алгори́тмов — раздел математики, изучающий общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. К задачам теории алгоритмов относятся формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т.п. Вместе с математической логикой теория алгоритмов образует теоретическую основу вычислительных наук, теории передачи информации, информатики, телекоммуникационных систем и других областей науки и техники.