por luis antonio santos e santos hace 3 años
647
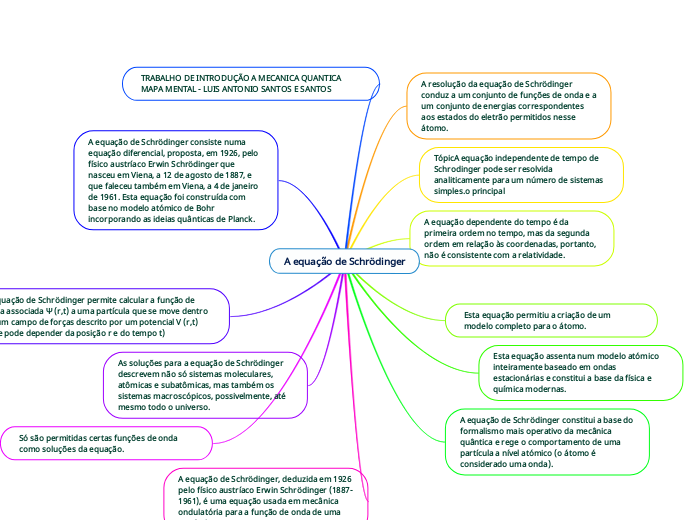
A equação de Schrödinger
A equação de Schrödinger é um pilar fundamental da mecânica quântica, descrevendo o comportamento das partículas a nível atômico através de funções de onda e estados de energia. Desenvolvida em 1926 pelo físico austríaco Erwin Schrödinger, a equação revolucionou a física e a química, fornecendo um modelo completo para o átomo e explicando fenômenos tanto em sistemas subatômicos quanto macroscópicos.