por Giuli C hace 9 años
173
Ver más
La geometría analítica estudia las figuras geométricas con técnicas básicas del análisis matemático y del álgebra en un sistema de coordenadas.
La probabilidad mide la frecuencia con la que ocurre un resultado en un experimento, bajo condiciones suficientemente estables.
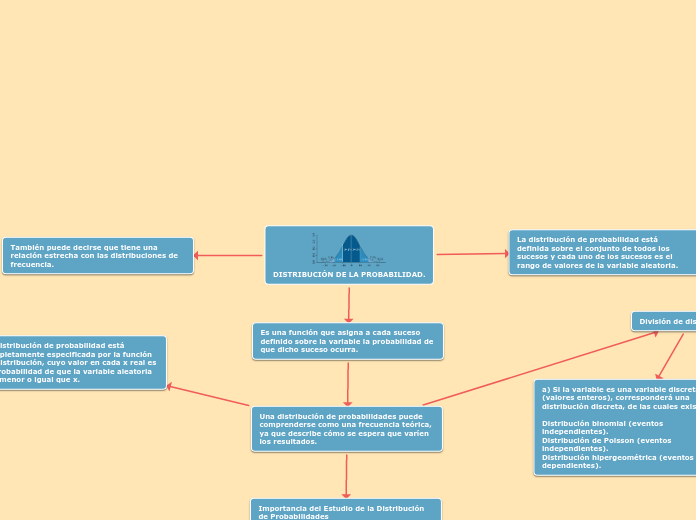
Teoría de la Probabilidad
Se usa extensamente en áreas como la estadística, la matemática, la ciencia y la filosofía para sacar conclusiones sobre la probabilidad de sucesos potenciales y la mecánica subyacente de sistemas complejos.
La teoría geométrica de números incorpora todas las formas de geometría.
Publicó su primer trabajo sobre la adición de cardinales transfinitos
Fue el primero en ofrecer respuestas a esta Teoría
Su obra "Principia Mathematica" es un conjunto de tres libros con las bases de la matemáticas, que tiene la teoría de conjuntos, números cardinales, números ordinales y números reales.
Es una función matemática usada como núcleo de un operador lineal integral y usada en la resolución de ecuaciones diferenciales no homogéneas con condiciones de contorno especificadas
