por Kézia Lôbo hace 1 año
90
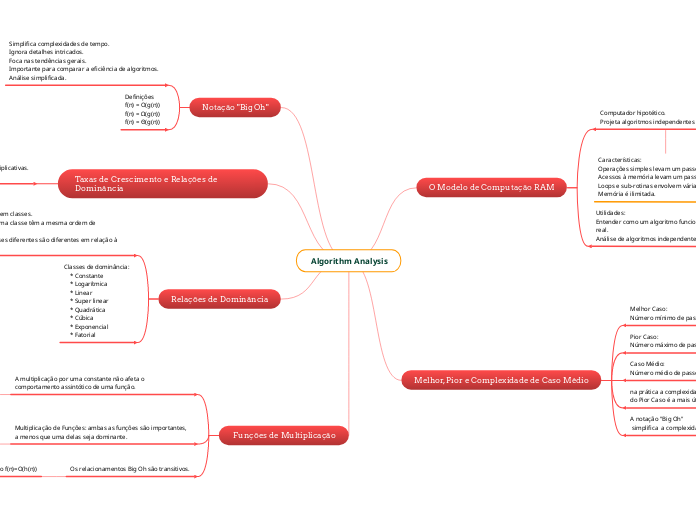
Algorithm Analysis
Analisar algoritmos é essencial para entender sua eficiência e comparar diferentes abordagens. A notação Big Oh é uma ferramenta crucial que simplifica as complexidades de tempo, focando nas tendências gerais e ignorando detalhes intricados.