Teaching and Assessing
Students with Exceptionalities
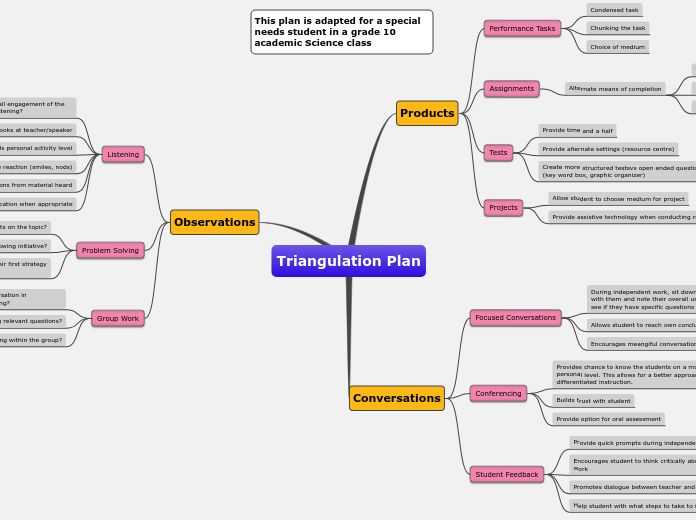
Planning for
Students Who Are
Mathematically
Gifted
Creativity
Presenting open-ended problems and investigations students can use divergent thinking to examine mathematical ideas-often in collaborations with others.
Creativity provides different options for students un culminating performances of their understanding, such as demonstrating their knowledge through interventions, experiments, simulations, etc.
Complexity
Increase sophistication of a topic
by raising the level of complexity or
pursuing greater depth to content,
possibly outside of the regular curriculum
or by making interdisciplinary connections.
Depth
Enrichment activities go into depth
beyond the topic of study to content
that is not specifically a part of your
grade-level curriculum but is an
extension of the original mathematical
tasks.
Acceleration
& Pacing
Allowing students to increase
the pace of their own learning
can give them access to curriculum
different from their grade level while
demanding more independent study.
When gifted students are accelerated through
the curriculum they are more likely to explore STEAM.
Pre-assessing students by
curriculum-based tests and also other
measures such as concept maps prior to
instruction allows the evaluation of what the
student already knows and in some cases identifies
how many grade levels ahead they might be.
Diverse
Learners
Addressing the needs of ALL
means providing access &
opportunity for:
* Who are identified as struggling
or having a disability.
* Who are mathematically gifted.
* Who are unmotivated or need to build
resilience.
Essential in making decisions about
how can you adapt instruction to meet
individual learner's need is the use of the
environment or the learner; it does not
alter the task.
Students backgrounds
are important not only for
who they are, but who they
are as learners which enriches
the classroom.
Students need opportunities
to advance their knowledge
supported by teaching that gives
attention to their individual learning
needs.
Prevention
Models
Progress
Monitoring
Combining instruction with
short daily assessments.
Assess students'
growth toward fluency
in basic facts.
Collect evidence of students'
knowledge of concepts through the
use of diagnostic interviews.
Response to
Internvention
Each tier in the
triangle represents a level
of intervention with
corresponding monitoring
of results and outcomes.
Tier 3: Represents students who need
need more intensive assistance, which
may include comprehensive mathematics instruction or a referral for special education evaluation or special education services. Individual student. 1-5%
Tier 2: Represent students who did not
reach the level of achievement expected during Tier 1 instruction. Small groups. 5-10 %
Tier 1: Represents the core
of all students based on high-quality mathematics curriculum, highly engaging instructional practices (ex: manipulatives, conceptual emphasis, etc.) & progress monitoring assessments. 80-90%
Multitiered student support
system often representd in a
three-tier triangle format.
Multitiered models are centered
on the three interwoven elements:
Formative
Assessment
Instructional
Support
(Internventions)
High-quality
Curriculum
Strategies to
Avoid
*Assigning more of the same work.
*Giving free time to early finishers.
* Assigning gifted students to help
struggling learners.
* Providing gifted pull-out opportunities.
*Offering independent enrichment
on the computer.
Adaptations for
Students with
Moderate/Severe Disabilities
When possible content should be connected to
life skills and features of jobs. Other times, link
mathematical learning objectives to everyday events
in a practical way.
Need extensive modifications and
individualized supports to learn
mathematics. Students included
are those with sever autism, sensory
disorders, limitations affecting movement,
cerebra palsy, & processing disorders (intellectual
Teaching & Assessing Students with Learning Disabilities
Phase 3: Provide Clarity.
Repeat the timeframe, ask students to share their thinking, emphasize connections, adapt delivery modes, emphasize the relevant points, support the organization of written work, & provide examples and nonexamples.
Phase 4: Consider Alternative
Assessments. Propose alternative products,
encourage self-monitoring & self-assessment,
& consider feedback charts.
Phase 5: Emphasize Practice & Summary.
Consolidate Ideas & Provide extra practice.
Students with learning disabilities often have
very specific difficulties with perceptual or cognitive
processing that may affect memory; general strategy use; attention; the ability to speak or express ideas in writing; ability to perceive auditory, visual, or written; ability to intregate
Phase 1: Structure the Environment.
Centralize attention, avoid confusion, & create smooth transitions.
Phase 2: Identify and Remove
Potential Barriers. Help students
remember, provide vocabulary &
concept support, use "friendly" numbers,
vary the task size, & adjust the visual display.
Implementing
Interventions
Think-Alouds
Your goal is always
to work toward high
student responsibility
for learning.
Instructional strategy you demonstrate the steps
to accomplish a task while verbalizing the thinking
process & reasosing that accompany the actions.
Peer-Assisted
Learning
Students learn best when they are placed
in the role of an apprentice working with
a more skilled peer or "expert".
Having students with disabilities "teach"
others is an important part of the learning
process.
Concrete,
Semi-Concrete, Abstract
(CSA)
Reflects concrete representations
such as manipulative materials
that encourage learning through
movement or action to semi-concrete
representations of drawings or pictures
learning through abstract symbols.
Includes modeling the
mental conversations that
go on in your mind as you
help students articulate
their own thinking.
Explicit Strategy
Instruction
Must include making
mathematical relationships
explicit.
Concrete models can
support explicit strategy
instruction.
Characterized by highly
structured, teacher-led
instruction on a specific
strategy.