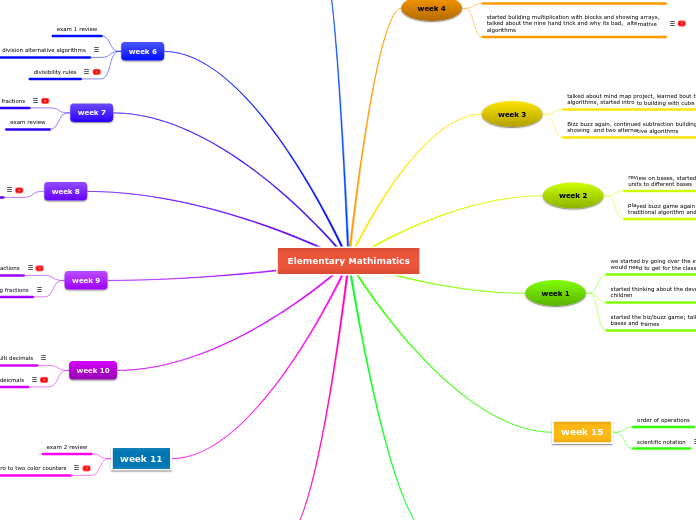
Elementary Mathimatics
week 13
solving integers adding/subtracting
SOLVE
integer adding :
example
-6+(-4)
6 is bigger (bigger group) - -
4 is smaller (smaller group) -
6+4=10
-10 answer!
- circle two
- different symbols = subtract
- same symbols = addition
- symbol left over is sign for answer (negative or positive)
Hectors method
integer subtracting:
example
-8-(-4)
- KCC!
- keep change change
- keep -8
- change the subtraction to addition
- change -4 to positive 4
-8+4
-8 bigger group - -
4 smaller group +
8-4= 4
4 answer!
- different symbol = subtract
- left over symbol is positive give to answer
showing integers adding/subtracting
adding show:
example:
-3+(-5)
- - - - - - - -
= -8
example :
3+(-2)
(+ +) +
(- - )
= 1
underline starting
blue answer
red adding/subtracting
add in the negatives or positives as you need then
subtracting show:
example
-3-(-4)
+(+)
<~ - - - - (-)
zero pairs: if you don't have enough to subtract add in some zeros! and create a zero bank for the extras
week 11
intro to two color counters
two color counters:
help build integers
red = negative
yellow/ other color ( not red) = positive
yellows on top because positive always goes on top
red on bottom because negative always goes below
zero bank: a positive and negative together (or multiple)
exam 2 review
week 10
solving deicmals
Add whole numbers: combine the two
Sub whole number: whole number to mixed number (denominator same fraction)
Sub mixed mixed: sub whole first multiply denominator for same, then subtract.
Add mixed mixed: add whole first, same denominator; then add.
Multi: find factors for funky 1 for simplify, multiply across.
Mixed by mixed: backwards "C" multi denom by whole, add to num (funky 1 last)
Divide: keep change flip (multiply by the reciprocal)
show add/sub/multi decimals
showing:
uses squares cuts them up , each long is a tenth each cube a hundredth
add:
put them together, divide them up in one square and add them up vertical tenth horizonal hundredth
sub:
same principles as addition but instead of adding them up divide the first one them circle the amount of the second one and "take away"
multiply:
same thing as add and sub but your gonna overlay them
the parts that are overlaid by both are the answer.
vertical first number horizontal second number
week 9
building/showing fractions
circle fractions are easiest to understand but you need to change to rectangle for bigger ones so students don't get confused.
set model: name items (color ,shape , etc.)
1/3 is blue
8/10 are circles
length model: size, length comparison
pencil 1/2 longer pen
john 2/5 the height of Emily
area model: fraction to area comparison (on top)
red 1/2 of yellow
purple is 2/3 green
multiplying fractions/dividing fractions
- Adding whole numbers to fractions: you just combine the two for your answer.
- Subtracting whole number from a fraction: you will need to make the whole number into a mixed number with the same denominator as the fraction.
- Subtracting mixed number by mixed number: you subtract whole numbers first then multiply to get same denominator, then subtract.
- Adding mixed numbers with mixed numbers: you add whole numbers together then work on finding the same denominator; then add.
- Multiplying fraction by fraction: work with numerator to denominator to find factors for Funky 1 to simplify, then multiply across.
- Mixed number multiplied by mixed number: Do the backwards "C" to multiply denominator by whole number then add to numerator. Then funky 1.
- Dividing fraction by fraction: use KEEP, CHANGE, FLIP (multiply by the reciprocal),
week 8
solving fractions
building:
place on top of each other for both add and sub
add:
(improper fractions)
multiply then add
circles for each whole number
pie divide into for fraction part
for both add and sub (need both denominator to be same in order to do problem)
show:
use rectangles to show: 3 rec
use rectangles to show : 2rec
week 7
exam review
division wrap up/ intro to fractions
numerator = number pieces have
denominator = how many pieces total/size of pieces
started comparing: which fraction is bigger, smaller, or equal
(1/2 helps)
(anchor fractions)
(butterfly method)
multiply numerator by 2
ex: 7/13 or 11/23
7(2)= 14 more than 13
11(2)= 22 less then 23
week 6
divisibility rules
divisibility rules: help learn what number are factors for high level math
2
even #s
end in 0,2,4,6,8
3
the sum of the digits
is / by 3
4
if the last 2 digits are / 4 then yes
5
last digit is 5 or 0
6
if 2 and 3 work 6 works
8
if last 3 digits /
9
the sum of digits / 9
10
last digits is 0
division alternative algorithms
trad division:
Students will have a hard time knowing where numbers goes( big # not on the outside)
repeat sub:
figure out the highest the student knows of the factors and write it on the side then subtract and keep repeating. Remainder goes in the numerator and the outside number is the denominator. PRO: students can start with what they have/know and be motivated to do faster. CONS: write it wrong and difficulty what to do with the remainder.
up division:
Write the equation how you say it just vertically (like a fraction). Writing the numbers spaced out to be able to write other numbers in between. Figure out how many times the denominator can go into the numerator; write in answer spot. Then multiply it to subtract from the first digit then divide again for the next digit. Remainder is the numerator and the denominator stays the same. CON: student needs to be good at math facts.
exam 1 review
week 5
learned subtraction alternative algorithms almost the same as addition, expanded form, equal addends
equal addends: both number add up to a friendly number so you don't have to carry
learned automaticity, the order to learn the multiplication table, why timed test are bad, practiced more with the alternative algorithms
Automaticity is the ability to do things without occupying the mind with the low-level details required, allowing it to become an automatic response pattern or habit. It is usually the result of learning, repetition, and practice.
your start with "red" easy ones 1,2,5,10
"blue" medium 3,9,doubles (4(4))
"green" hard 4,6,7,8
week 14
multiplying/ dividing integers
show :
create groups
for positive create circles then add in the symbols for the integers inside
total them up for answer
for negative do same as before with add/subtract create zero pairs and group up the symbols then arrows for taking away.
left over is answer
multiplication and division:
(negative and negative NOT equal to positive)
neg times neg = positive!
- same sign answer is positive
- different sign answer is negative
example
-60(30)
different sign = neg
60(30)=1800
-1800 answer!
(same for division)
week 15
scientific notation
scientific notation:
the decimals need to be between 1-10
negative exponent = very small number
positive exponent = very big number
standard form number bigger than 1 = positive exponent
standard form number written as decimal = negative exponent
2.15x10^-4 = small number/ decimal
5.873 x 10^6 = big number
0.000467 = neg exp
4.67x10^-4
3470000= pos exp
3.47x10^6
order of operations
shows how to tell the sign of exponents add a zero!
examples
0-4^2=0-8=-16
0+(-4)^2=0+16=16
0-(-4)^2 =0-16=-16
order of operations:
NO p e m d a s!
also not horizontal go vertical
Groups
Exponents
M/D from L-> R
A/S from L -> R
groups go along with parenthesis and are separated by addition and subtraction symbols
A) -4+7(2)-8^2
group -4= -4
group 7(2)= 14
group 8^2 =64
left to right
-4+14= 10
10-14= -4
-4 answer!
week 1
started the biz/buzz game; talked more about other kinds of bases and frames
frames are used when a students fills it up usually with block and it counts to ten a five is used a stepping stool to then ten frame,
there are different bases, normal every day bases are base 10. base 5 is when you have five units it makes one long five longs make a flat etc..
started thinking about the developments for math in young children
(early number sense) Cardinality, when they finish counting a group they will know how many are in that group with out needed to count a again.
one to one correspondence: each number goes with one item they are touching
counting more and less,
subitizing: they can look at a group and tell how many are in it just by looking at it without counting.
. then a basic intro to bases.
cube, long, flat, cube, long, flat
one, ten, hundred,
we started by going over the syllabus and the material that we would need to get for the class
week 2
played buzz game again talked about the flaws of the traditional algorithm and alternative algorithms for addition
traditional algorithm not based of prior knowledge and confusing for some students.
alternative algorithms:
expanded form, left to right, friendly numbers/trading off,
scratch, lattice
review on bases, started using blocks to build conversions of units to different bases
week 3
Bizz buzz again, continued subtraction building, started showing and two alternative algorithms
the two alternative algorithms:
expanded form very similar to addition expanded from and equal addends
talked about mind map project, learned bout two new algorithms, started intro to building with cube subtraction
week 4
started building multiplication with blocks and showing arrays, talked about the nine hand trick and why its bad, alternative algorithms
the nines are bad because it doesn't help the fins patterns and wont help them understand higher math
alternative algorithm:
expanded form
left to right
area model
lattice
started multiplication, talked about the importance of understanding what it means not just the answers, three different models of multiplication
it important that kids know that 4(7) is different from 7(4) they have the same answer but one is four groups of seven and the other seven groups of four!
models:
groups
arrays
area