Error tipo I
Si usted rechaza la hipótesis nula cuando es verdadera, comete un error de tipo I. La probabilidad de cometer un error de tipo I es α, que es el nivel de significancia que usted establece para su prueba de hipótesis. Un α de 0.05 indica que usted está dispuesto a aceptar una probabilidad de 5% de estar equivocado al rechazar la hipótesis nula. Para reducir este riesgo, debe utilizar un valor menor para α. Sin embargo, usar un valor menor para alfa significa que usted tendrá menos probabilidad de detectar una diferencia si está realmente existe.
Hipótesis alternativa
La hipótesis alternativa es aquella que indica que un parámetro de población es más pequeño, más grande o diferente del valor hipotético de la hipótesis nula. La hipótesis alternativa es lo que usted podría pensar que es cierto o espera probar que es cierto.
Hipótesis nula
La hipótesis nula (H0) es una hipótesis que el investigador trata de refutar, rechazar o anular. La hipótesis nula es aquella que indica que un parámetro de población (tal como la media, la desviación estándar, etc.) es igual a un valor hipotético. La hipótesis nula suele ser una afirmación inicial que se basa en análisis previos o en conocimiento especializado.
Una prueba de hipótesis es una regla que especifica si se puede aceptar o rechazar una afirmación acerca de una población dependiendo de la evidencia proporcionada por una muestra de datos
Error tipo II
Cuando la hipótesis nula es falsa y usted no la rechaza, comete un error de tipo II. La probabilidad de cometer un error de tipo II es β, que depende de la potencia de la prueba. Puede reducir el riesgo de cometer un error de tipo II al asegurarse de que la prueba tenga suficiente potencia. Para ello, asegúrese de que el tamaño de la muestra sea lo suficientemente grande como para detectar una diferencia práctica cuando está realmente exista.
Nivel de Significancia
El nivel de significancia, también denotado como alfa o α, es la probabilidad de rechazar la hipótesis nula cuando es verdadera. Por ejemplo, un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe una diferencia cuando en realidad no hay ninguna diferencia.
Potencia de la prueba de hipótesis
La potencia de una prueba de hipótesis es la probabilidad de que la prueba rechace correctamente la hipótesis nula. La potencia de una prueba de hipótesis se ve afectada por el tamaño de la muestra, la diferencia, la variabilidad de los datos y el nivel de significancia de la prueba.
Si una prueba tiene poca potencia, es posible que usted no detecte un efecto y concluya erróneamente que no existe ninguno. Si la potencia de una prueba es demasiado alta, efectos muy pequeños y posiblemente sin importancia podrían parecer significativos.
Estadístico de prueba
Un estadístico de prueba es una variable aleatoria que se calcula a partir de datos de muestra y se utiliza en una prueba de hipótesis. Puede utilizar los estadísticos de prueba para determinar si puede rechazar la hipótesis nula. El estadístico de prueba compara sus datos con lo que se espera bajo la hipótesis nula. El estadístico de prueba se utiliza para calcular el valor p.
Valor p o p Value
Es la probabilidad de que un valor estadístico calculado sea posible dada una hipótesis nula cierta. En términos simples, el valor p ayuda a diferenciar resultados que son producto del azar del muestreo, de resultados que son estadísticamente significativos.
Si el valor p cumple con la condición de ser menor que un nivel de significancia impuesto arbitrariamente, este se considera como un resultado estadísticamente significativo y, por lo tanto, permite rechazar la hipótesis nula.
Medidas de forma
permiten comprobar si una distribución de frecuencia tiene características especiales como simetría, asimetría, nivel de concentración de datos y nivel de apuntamiento que la clasifiquen en un tipo particular de distribución.
Curtosis
analiza el grado de concentración que presentan los valores alrededor de la zona central de la distribución.
Asimetría
El concepto de asimetría se refiere a si la curva que forman los valores de la serie presenta la misma forma a izquierda y derecha de un valor central (media aritmética)
Fundamentos de estadística descriptiva y Probabilidad.
Distribución Normal estándar
es una distribución con forma de campana donde las desviaciones estándar sucesivas con respecto a la media establecen valores de referencia para estimar el porcentaje de observaciones de los datos. Estos valores de referencia son la base de muchas pruebas de hipótesis, como las pruebas Z y t.
histograma
Un histograma es la representación gráfica en forma de barras, que simboliza la distribución de un conjunto de datos. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o de la muestra, respecto a una característica, cuantitativa y continua.
Diagrama de cajas
son una presentación visual que describe varias características importantes, al mismo tiempo, tales como la dispersión y simetría.
Para su realización se representan los tres cuartiles y los valores mínimo y máximo de los datos, sobre un rectángulo, alineado horizontal o verticalmente.
Medidas de dispersión
Las medidas de dispersión tratan, a través del cálculo de diferentes fórmulas, de arrojar un valor numérico que ofrezca información sobre el grado de variabilidad de una variable
Coeficiente de variación
Su cálculo se obtiene de dividir la desviación típica entre el valor absoluto de la media del conjunto y por lo general se expresa en porcentaje para su mejor comprensión.
Desviación típica
La desviación típica es otra medida que ofrece información de la dispersión respecto a la media. Su cálculo es exactamente el mismo que la varianza, pero realizando la raíz cuadrada de su resultado. Es decir, la desviación típica es la raíz cuadrada de la varianza.
Varianza
La varianza es una medida de dispersión que representa la variabilidad de una serie de datos respecto a su media. Formalmente se calcula como la suma de los residuos al cuadrado divididos entre el total de observaciones
Rango
El rango es un valor numérico que indica la diferencia entre el valor máximo y el mínimo de una población o muestra estadística. Su fórmula es:
R = Máxx – Mínx
Medidas de posicion
parámetros estadísticos que dividen a la población en otras cuantías distintas.
Los cálculos son similares a los de la mediana, variando la posición a buscar y el intervalo en el que se encuentra el cuantil.
Percentiles
Tenemos 99 percentiles que dividirían a la población en 100 partes iguales, denotados por P1, P2, ..., P98, P99.
Los percentiles 25, 50 y 75 coinciden con los cuartiles.
Deciles
Dividen la distribución de datos en 10 partes iguales, correspondiendo cada uno al 10% de los datos. Tendríamos, por tanto, nueve deciles que denotamos por D1, D2, D3, ..., D9
El quinto decil coincide con la mediana.
Cuartiles
Dividen a la población de datos en cuatro partes iguales, correspondiendo cada uno de ellos al 25% de los datos. Tenemos por tanto tres cuartiles que denotamos como Q1, Q2, Q3, y se les llama primer, segundo y tercer cuartil.
El segundo cuartil coincide con la mediana.
Medidas de Centralización
Las medidas de centralización o de tendencia central expresan el valor en torno al cual se sitúan los datos de una muestra.
Mediana
La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.
Moda
La moda es el dato más repetido, el valor de la variable con mayor frecuencia absoluta. En cierto sentido la definición matemática corresponde con la locución "estar de moda", esto es, ser lo que más se lleva
Media
La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos. Se le llama también promedio o, simplemente, media.
Datos
es la información recopilada de las variables de los elementos como resultado de estudio de un fenómeno o proceso.
cuantitativos
En una dato cuantitativo la información es reportada numéricamente. Los datos cuantitativos pueden ser discretos o continuos
cualitativos
Cuando la característica o variable en estudio es no numérica, se le denomina dato cualitativo o de atributo.
Variable
Es cada una de las características o cualidades poseen los individuos de una población.
Independiente
los valores de este tipo de variables no dependen del de otras, son representadas en el eje de las abscisas y en las funciones con la letra X.
Cualitativas
hace alusión a aquellas cualidades que no se las puede medir numéricamente.
Aleatorias
son aquellas funciones que asocian un número real a cada elemento del espacio muestral E
aleatoria binominal
con esta variable se muestra el número de éxitos que se adquirieron en cada prueba de un experimento. Es como la discreta, que sólo adquiere valores enteros, pero de acuerdo a las pruebas realizadas.
aleatoria continua
a diferencia de la discreta, puede adquirir cualquier valor dentro de un intervalo de la recta real.
aleatoria discreta
esta variable solamente puede adquirir valores enteros.
ordinal
en este tipo de variables, en cambio, las modalidades numéricas no pueden ser ordenadas bajo ningún criterio.
ordinal o cuasicuantitativa
este tipo de variables presentan modalidades no numéricas en las que hay un orden
Cuantitativas
estas variables se expresan por medio de un número, lo que permite utilizarlas para operaciones aritméticas.
Discretas
esta variable no puede adquirir valores intermedios entre dos números, sino aislados.
Continuas
este tipo de variables puede adquirir valores existentes entre dos números.
Individuo
Un individuo o unidad estadista es cada uno de los elementos que componen la población.
Subconjunto finito de una población. El número de elementos que forman la muestra se denomina tamaño muestral.
Conjunto finito o infinito de elementos, sobre los que realiza observaciones.
Probabilidad
La probabilidad es el cálculo matemático que evalúa las posibilidades que existen de que una cosa suceda cuando interviene el azar.
Estadística descriptiva
Es la rama de la estadística que recolecta, analiza y caracteriza un conjunto de datos, con el objetivo de describir las características y comportamientos de este conjunto mediante medidas de resumen, tablas o gráficos.
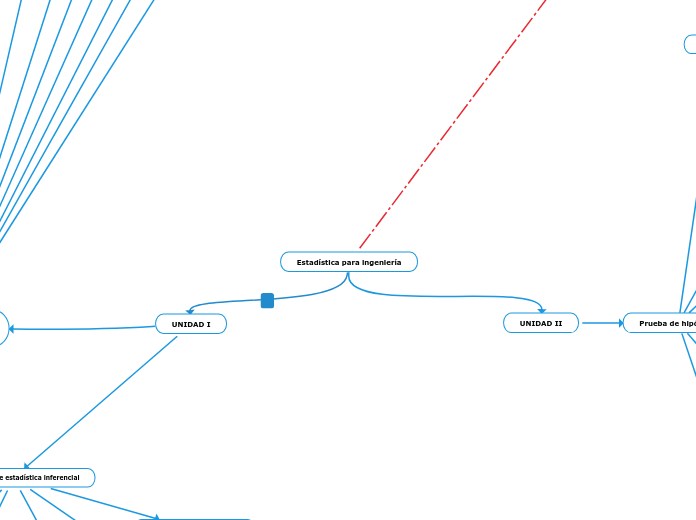
UNIDAD II
Prueba de hipótesis
UNIDAD I
Fundamentos de estadística inferencial
Intervalo de confianza
es un rango de valores, derivado de los estadísticos de la muestra, que posiblemente incluya el valor de un parámetro de población desconocido. ubtopic
Teorema del límite central.
describe la distribución de la media de una muestra aleatoria proveniente de una población con varianza finita.
Muestreo por conglomerados
La unidad muestral es un grupo de elementos de la población que forman previsiblemente una unidad de comportamiento representativo. Dicha unidad es el conglomerado cuyo comportamiento interno puede ser muy disperso (varianza grande) pero que presumiblemente poseerá un comportamiento próximo a otros conglomerados (varianza entre conglomerados , pequeña). Los conglomerados se estudian en profundidad hasta conseguir el tamaño muestral adecuado.
Muestreo aleatorio estratificado
Consiste en considerar categorías típicas diferentes entre sí (estratos) que poseen una gran homogeneidad interna (poca varianza interna) y no obstante son heterogéneos entre sí (mucha varianza entre estratos) . La muestra se distribuye ( se extrae de ) entre los estratos predeterminados según la naturaleza de la población (ejemplo : sexo , lugar geográfico,etc.).
Muestreo aleatorio sistemático
Esta técnica consiste en extraer elementos de la población mediante una regla sistematizadora que previamente hemos creado (sencillamente cada K elementos) . Así ; numerada la población , se elige(aleatoriamente) un primer elemento base , partiendo de éste se aplica la regla para conseguir los demás hasta conseguir el tamaño muestral adecuado . Este procedimiento conlleva el riesgo de dar resultados sesgados si en la población se dan periodicidades o rachas .
Estadistico
Es el elemento que describe una muestra y sirve como una estimación del parámetro de la población correspondiente.
Muestra
La muestra es una pieza de la población a estudiar que sirve para representarla.
Parámetro
Se llama parámetro a un valor representativo de una población, como la media aritmética, una proporción o su desviación típica.
Población
Una población se precisa como un conjunto finito o infinito de personas u objetos que presentan características comunes, "Una población es un conjunto de todos los elementos que estamos estudiando, acerca de los cuales intentamos sacar conclusiones".
Estadística para ingeniería
INTEGRANTES
• Esparza Aguilar Arlette Naomi
• Hernández Gutiérrez Laura Leticia
• Ibarra Ruíz Ana Patricia
• Pedroza López Jesús Antonio
• Ramírez Ramos Patricia
• Ramos Carillo José