por Jonathan Ivan Llamas Salazar hace 9 años
2130
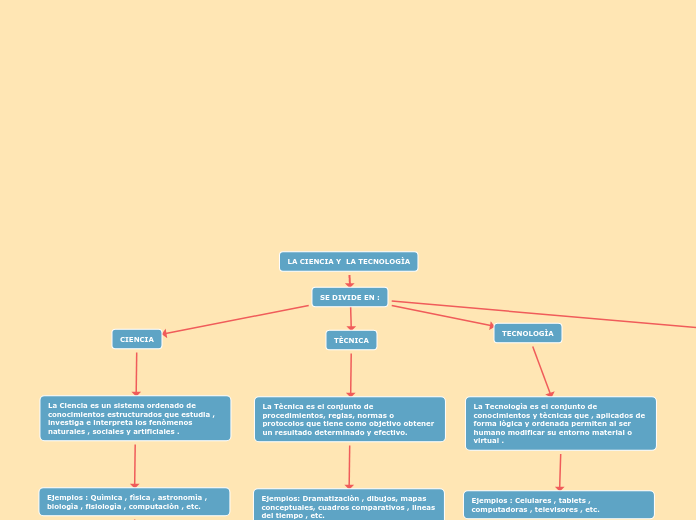
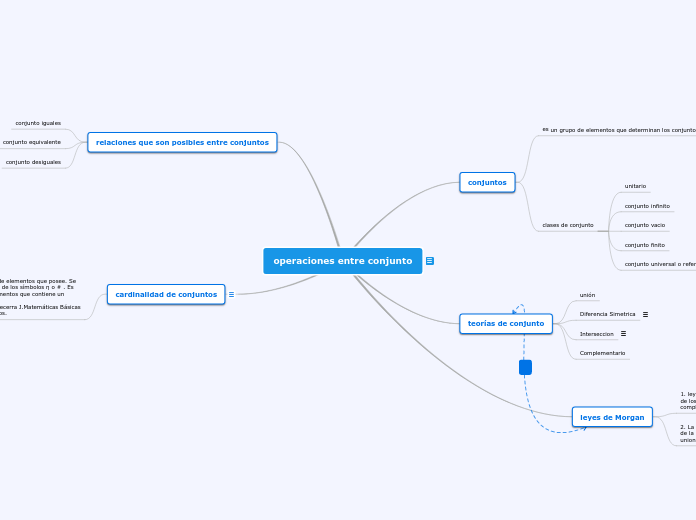
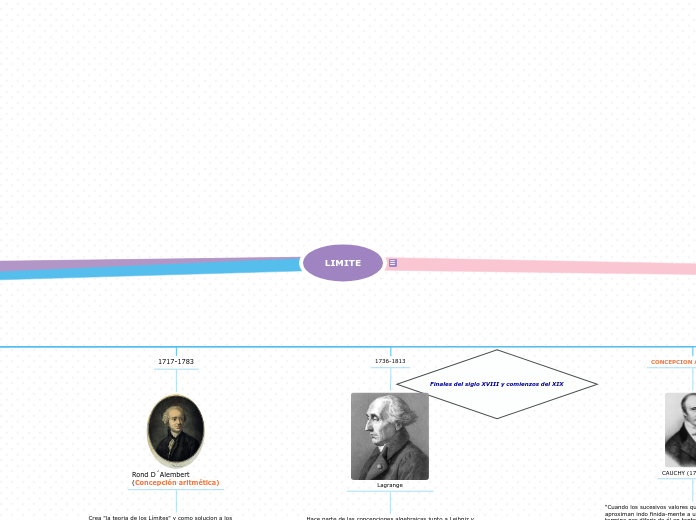
Funciones, Modelos y Limites
En matemáticas, una función se define como una relación entre dos conjuntos, denominados A y B, donde cada elemento de A se asocia de manera única a un elemento de B. Este vínculo, sin embargo, no requiere que cada elemento de B se relacione con un único elemento de A, permitiendo que un mismo elemento de B pueda estar asociado a múltiples elementos de A.