por Andres Alberto Mompotes Hernandez hace 3 años
178
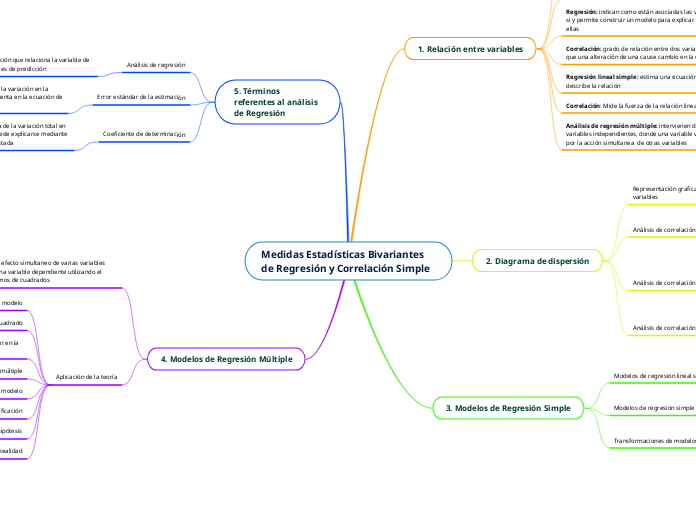
Medidas Estadísticas Bivariantes de Regresión y Correlación Simple
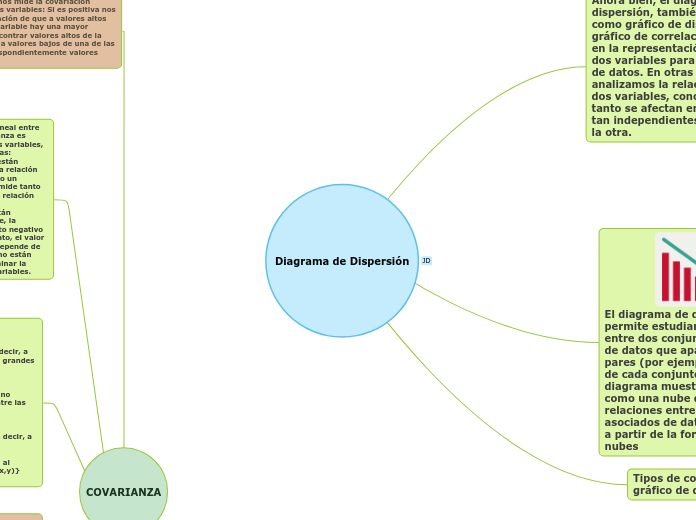
El análisis estadístico bivariante se enfoca en la relación entre dos variables a través de modelos de regresión y correlación simple. La regresión simple puede ser lineal o no lineal, usando modelos como el exponencial, cúbico o cuadrático.