Paying Attention to Fractions-002 Group 3

Ver más

Fractions, Decimals, and Percentages

por Bailey Huylar

frazioni quotidiane

por Carolina Jimenez

What you are going to learn next week

por Marco Bertolini

Curation in Education: Great Examples

por Robin Good

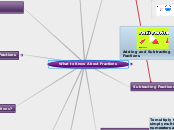
Introducing Fractions-Section 1 by Loe G.B. 1. 5 TYPES OF FRACTIONS (note: numerator and denominator could also be negative.)

Complex* Fractions

Definition: Either or both the numerator and the denominator are fractions.

Improper Fractions

Definition: Digits in both the numerator and the denominator are integers; the numerator > the denominator.

Mixed Fractions

Definition: A quantity represented by an integer and a proper fraction

Unit Frations

Definition: Digits in both the numerator and the denominator are integers; the numerator = 1.

Proper Fractions

Definition: Digits in both the numerator and the denominator are integers; the numerator < the denominator.

Simple Fractions

Definition: Digits in both the numerator and the denominator are integers; the denominator ≠ 0.

Examples

Paying Attention to Fractions-002 Group 3

4 Constructs: Lexia Simmons

Operator

Use of a fraction to enlarge or shrink a quantity by a factor Fraction reduces or increases a quantity

Quotient

Dividing the numerator by the denominator Equal Sharing Result is the decimal equivalent for the fraction››

The Denominator indicates the number of items that are in one part of the set The Numerator indicates the number of items that are in the other part of the set Adding the numerator and the denominator together determines the fraction unit being used to partition, or divide, the set.

Part-Whole Relationships

Denominator indicates the fractional unit being used Numerator indicates the number of fractional units being counted

Main topic

How Can We Promote Fractions Thinking? (Olivia Sieczkowski)

-Create a strong base for using operations throughout P/J grades( i.e introduction of dollars and cents)
-Ensure prior essential knowledge of operations is in place before introducing fractions

Equivelence and Comparing

-Help students understand the difference between parts and wholes and to consider both the numerator and denominator when comparing fractions
-Help students connect to other number systems besides division

Representations

- Introduce pictures and notational representations at the same time
- Provide familiar representations to new fraction concepts
- Provide similar representation throughout multiple grade levels (number lines, volume)
- Avoid introducing circles in P/J grades

-Counting from 0-1, in each individual unit which helps students understand the relationship between parts and wholes
-Introduce mixed and proper fractions at the same time
-use precise language

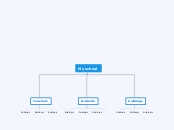
3. Models that should be used (Jasmine)

Using Models

When students using models it will help them test and develop predictions about the relationships within the fractions.

When using models the students have to make sure the whole remains unchanged. Which means the selection of model is important that the whole will not be spilt. Number lines are a good example to make sure that the whole is preserved.

Using models to compare fractions like a rectangle or a number line.

Allow students to use models to determine equivalent fractions.

Different types of Models

Area Model: a shape that represents the whole. With the fractional regions being equal in area they may not all be congruent.
Set Model: A bunch of items that represents the whole amount. Subsets of the whole make up fractional parts.
Volume Model: when a three-dimensional figure represents the whole. This whole would be divided into fractional regions that are occupied by space within the figure.

Part-Part Relationships

Number Line Model

2. Why is Understanding Fractions Importans (Ashley S.)

Building a Foundation

Understanding fractions allows students to build a foundation to develop an understanding for more complex mathematical concepts (e.g., proportionality and ratio, linear relationships, trigonometry, and radial measure)

Daily Life

Understanding fractions supports individuals in everyday activities (e.g., cooking, carpentry, sewing, etc.)
Not understanding fractions can cause difficulties in adulthood (e.g., failure to understand medication regiments)

3 Models that should be used (Eduardo)

Volume Model

a three-dimensional figure represents the whole. The whole is divided into fractionalregions that are occupied by space within the figure.

Set Model

a collection of items represents the whole amount. Subsets of the whole make up thefractional parts.

Area Model

one shape represents the whole. The whole is divided into fractional regions.

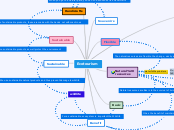
Key Concepts - Section 4 by Sarah C.

Operations

Students need a conceptual understanding of equivalency, estimating, unit fractions, and part-whole relationships to understand operations When these concepts are explored meaningfully, students develop an implicit understanding. For example, students may realize that 3/4 = 1/4 + 1/4 + 1/4

Comparing and Ordering

Deciding which of the relations is equal to, is than, or is greater than Students can use models, benchmarks, common numerators, equivalent fractions and/or unit fractions to compare and order fractions

Equivalency

When determining equivalent fractions, students are identifying different fractional units that can be used to describe a quantity Example: 1/3 = 5/15 = 7/21

The Whole

The denominator provides information about how the whole has been divided Example: When considering 3/2 as a quotient, the 3 is the whole and the 2 shows the number of partitions

Unit Fractions

In part-whole fractions, the denominator indicates the fractional unit, or the number of equi-partitions of the whole being considered. Students develop flexibility in representing unit fractions by using physical models, pictures, and numbers.

6. Fractions Across Strands and Grades + Ministry Resources (Emma C.)

Resources

To aid in leaning and understanding fractions there are many wide ranging resources listed by the ministry. These resources vary from research articles, webcasts, educational documents and digital games.

Strands & Grades

Instructing fractions in a punctuated fashion (chucked), allows students to better comprehend fractions as a unit. While also allowing teachers to be responsive to students when planning additional activities. Students are then able to connect their understanding of fractions to other math units and concepts.