Probability and Counting Chart

Ver más

ENGLISH 3rd ESO

por David Perea

ingles - if claueses

por Douglas Angelo

Finding Probability

por Mandi Turner

PERUVIAN POLITICS

por Diana Elizabeth Apaza Mamani

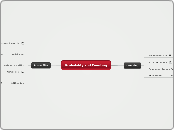
Probability and Counting

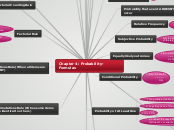
Probability

Addition Rule

Mutural Exclusive?

P(A or B) = P(A) + P(B) - P(both)

P(A or B) = P(A) + P(B)

Complement

"At least one" = one or more

-complement of getting at least one particular event means that you get NO occurance of that event.

P(A) and P(A -)

Conditonal Probability

P(B| A) = P(A & B) / P(A)

Mutiplication

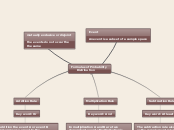
Independent?

No

Dependent

Dependent: if A & B are not independent

-selection without replacement

P(A & B) = P(A) * P(B| A)

P(B|A) = probability of event B occuring after event A

Yes

Independent

Independent: if occurance of events A and B does not affect the probability of the occurance of the other.

- with replacement

-5% rule

P(A) * P(B)

Classic and Realative Frequency Probability

P(E) = # of ways E occurs/ total # of outcomes

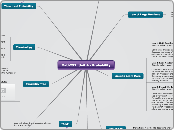
Counting

Factorial Rule

n!

n! = # of different permutations of 'n' different items when all 'n' of them are selected.

Fundamental Counting Rule

m * n

Combinations Rule

Combinations -are arrangements in which different sequences of the same items are not counted separately.

nCr = n! / ((n-r)!r!)

nCr = n! / ((n-r)!r!) = # of different combinations (order doesn't matter) when 'n' different items are available but only 'n' of them are selected without replacement.

Permutations Rule

Permutations are arrangements in which different sequences of the same items are counted separately

n! n1! n2!....nk!

n!n1!n2! ...nk! = # of different permutations when 'n' items are available and all 'n' are selected without replacement, but some items are identical to others.