por maria camila ospino martinez hace 3 años
419
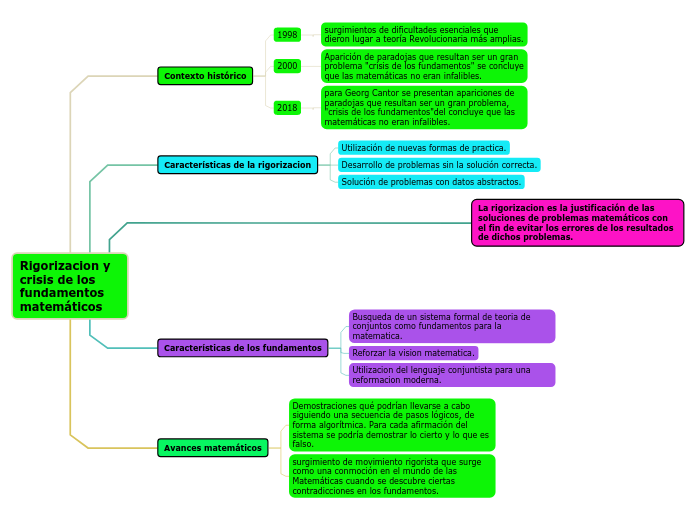
Rigorizacion y crisis de los fundamentos matemáticos
En el mundo de las matemáticas, surgió un movimiento rigorista debido a la aparición de contradicciones en sus fundamentos, lo que llevó a una crisis significativa. Este movimiento buscó justificar las soluciones de problemas matemáticos para evitar errores en los resultados.