Sistema de coordenadas
Name the character
Type in the name of the character whose change throughout the story you are going to analyze.
Example: Nick Carraway.
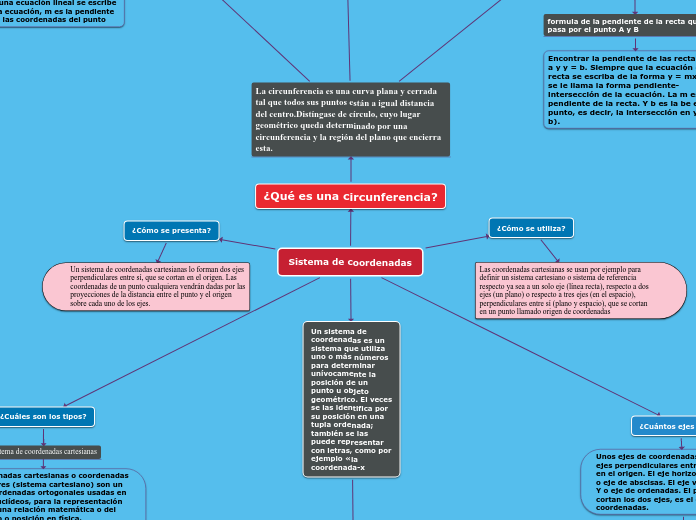
¿Qué es una circunferencia?
La circunferencia es una curva plana y cerrada tal que todos sus puntos están a igual distancia del centro.Distíngase de círculo, cuyo lugar geométrico queda determinado por una circunferencia y la región del plano que encierra esta.
Función
Operaciones con funciones.
Las funciones con dominios que se traslapan pueden ser sumadas, restadas, multiplicadas y divididas. Si f ( x ) y g ( x ) son dos funciones, entonces para todas las x en el dominio de ambas funciones la suma, diferencia, producto y cociente están definidos como sigue. Las operaciones de suma, resta, multiplicación y división entre funciones son posibles y semejantes a las correspondientes efectuadas con los números. Además, se define la composición de funciones.
Sean f (x) y g (x) son dos funciones definidas en un mismo intervalo cuyos dominios respectivos son y .
Composición de funciones.
una función compuesta es una función formada por la composición o aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante
Funciones inversas.
La función inversa (o función recíproca) de f (denotada por f-1) es aquella que hace el camino inverso, asignando a los elementos de Y elementos de X. También podemos definir una función inversa a partir de la composición de funciones. Para que una función f tenga inversa necesariamente debe ser inyectiva. En matemáticas, especialmente en análisis matemático, si f es una función que asigna elementos de I en elementos de J, en ciertas condiciones será posible definir la función f ⁻¹ que realice el camino de vuelta de J a I. En ese caso diremos que f ⁻¹ es la función inversa de f.
clases de funciones.
Funciones explícitas
Si se pueden obtener las imágenes de x por simple sustitución como en este ejemplo : f(x)=5x-2
Funciones implícitas
Si no se pueden obtener las imágenes de x por simple sustitución, sino que es necesario efectuar operaciones, como en este ejemplo 5x - y - 2 = 0
Además de esta clasificación, hay 6 otros tipos de funciones algebraicas
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
f(x)=a_0+a_1x+a_2x+a_3x+...+a_nx^{n}
Su dominio es {R} , es decir, cualquier número real tiene imagen
Funciones constantes
formas de representación
Dominio y rango
El dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma. Los dominios pueden también estar explícitamente especificados, si hay valores para los cuales la función pudiera estar definida, pero que no deseamos considerarlos por alguna razón.
Representación numérica
Para representar una función de forma numérica precisamos una tabla de valores en las que a cada valor de x, vemos que le corresponde uno de y. A la izquierda solemos encontrar número naturales y en la derecha la proyección del valor que le damos a x, aunque podemos poner cualquier valor que necesitemos.
Representación algebraica
Si queremos representar las funciones matemáticas de forma algebraica debemos explicar en qué consiste la función con una ecuación explícita que explique la relación que existe entre las dos magnitudes (x, y). De esta forma, podemos conocer las propiedades características de la función. y=mx + b
Representación visual
La forma visual de las funciones matematicas es la que se presenta mediante una gráfica en el eje cartesiano. Existen varios tipos de funciones y sus gráficas, que poseen diferentes propiedades según las características que poseen.
Definición
La definición general de función hace referencia a la dependencia entre los elementos de dos conjuntos dados. Dados dos conjuntos A y B, una función (también aplicación o mapeo) entre ellos es una asociación f que a cada elemento de A le asigna un único elemento de B.
¿A que llamamos punto pendiente de la recta?
Un tipo de ecuación lineal es la forma punto-pendiente, la cual nos proporciona la pendiente de una recta y las coordenadas de un punto en ella. La forma punto-pendiente de una ecuación lineal se escribe como. En ésta ecuación, m es la pendiente y (x1, y1) son las coordenadas del punto
¿Qué es una pendiente de recta entre dos puntos?
La pendiente es la inclinación de la recta con respecto al eje de abscisas. Se denota con la letra m. La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas.
formula de la pendiente de la recta que pasa por el punto A y B
Encontrar la pendiente de las rectas x = a y y = b. Siempre que la ecuación de la recta se escriba de la forma y = mx + b, se le llama la forma pendiente-intersección de la ecuación. La m es la pendiente de la recta. Y b es la be en el punto, es decir, la intersección en y(0, b).
¿Cuántos ejes tiene?
Unos ejes de coordenadas lo forman dos ejes perpendiculares entre sí, que se cortan en el origen. El eje horizontal se llama eje X o eje de abscisas. El eje vertical se llama eje Y o eje de ordenadas. El punto O, donde se cortan los dos ejes, es el origen de coordenadas.
¿Cómo se le llama a la coordenada X?
El eje horizontal se llama eje X o eje de abscisas.
¿Cuál es el nombre que tiene la coordenada Y?
El eje vertical se llama eje Y o eje de ordenadas.
¿Cuáles son los tipos?
Las coordenadas cartesianas o coordenadas rectangulares (sistema cartesiano) son un tipo de coordenadas ortogonales usadas en espacios euclídeos, para la representación gráfica de una relación matemática o del movimiento o posición en física, caracterizadas por tener como referencia ejes ortogonales entre sí que concurren en el punto de origen.
Sistema de coordenadas polares
El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un ángulo y una distancia.
Sistema de coordenadas log-polares
Es un sistema de coordenadas donde un punto se identifica con dos números, uno para el logaritmo de la distancia a un cierto punto y otro para un ángulo. Las coordenadas logarítmicas están estrechamente conectadas con las coordenadas polares, que generalmente se usan para describir dominios en el plano con algún tipo de simetría rotacional.
Sistema de coordenadas cilíndricas
El sistema de coordenadas cilíndricas es muy conveniente en aquellos casos en que se tratan problemas que tienen simetría de tipo cilíndrico o azimutal. Se trata de una versión en tres dimensiones de las coordenadas polares de la geometría analítica plana.
Sistema de coordenadas esféricas
Al igual que las coordenadas cilíndricas, el sistema de coordenadas esféricas se usa en espacios euclidianos tridimensionales. Este sistema de coordenadas esféricas está formado por tres ejes mutuamente ortogonales que se cortan en el origen. La primera coordenada es la distancia entre el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar la posición del punto.
Sistema de coordenadas cartesianas
Un sistema de coordenadas es un sistema que utiliza uno o más números para determinar unívocamente la posición de un punto u objeto geométrico. El veces se las identifica por su posición en una tupla ordenada; también se las puede representar con letras, como por ejemplo «la coordenada-x
¿A que llamamos distancia entre dos puntos?
¿Qué es un punto medio de un segmento de recta?
Punto medio en matemática, es el punto que se encuentra a la misma distancia de otros dos puntos cualquiera o extremos de un segmento. Más generalmente punto equidistante en matemática, es el punto que se encuentra a la misma distancia de dos elementos geométricos, ya sean puntos, segmentos, rectas, etc. Si es un segmento, el punto medio es el que lo divide en dos partes iguales. En ese caso, el punto medio es único y equidista de los extremos del segmento. Por cumplir esta última condición, pertenece a la mediatriz del segmento.
El punto medio de los puntos ( x1,y1) y (x2,y2) está dado por la siguiente fórmula:
(x1 + x2 , y1 + y2)
________ _________
2 2
En las matemáticas, la distancia entre dos puntos del espacio euclídeo equivale a la longitud del segmento de la recta que los une, expresado numéricamente. La distancia entre dos puntos está vinculada al plano cartesiano, ya que este permite calcular la distancia que existe entre ambos puntos, a partir de la ubicación de las coordenadas de ambos. Por su parte, cuando ambos puntos pasan del plano a la superficie terrestre, su distancia se calcula de otra manera. De acuerdo con la metodología denominada fórmula del Haversine.
FORMULA
Para calcular la distancia entre dos puntos usando la fórmula de la distancia, que es una aplicación del teorema Pitágoras. Podemos reescribir el teorema Pitágoras como d=√((x_2-x_1)²+(y_2-y_1)²) utilizada para calcular la distancia entre dos puntos.
EJEMPLO
Demostrar que los puntos : A(3, 8); B(-11, 3) y C(-8, -2) son vértices de un triángulo isósceles.
¿Cómo se presenta?
Un sistema de coordenadas cartesianas lo forman dos ejes perpendiculares entre sí, que se cortan en el origen. Las coordenadas de un punto cualquiera vendrán dadas por las proyecciones de la distancia entre el punto y el origen sobre cada uno de los ejes.
¿Cómo se utiliza?
Las coordenadas cartesianas se usan por ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas