por Yureika Medrano hace 6 años
365
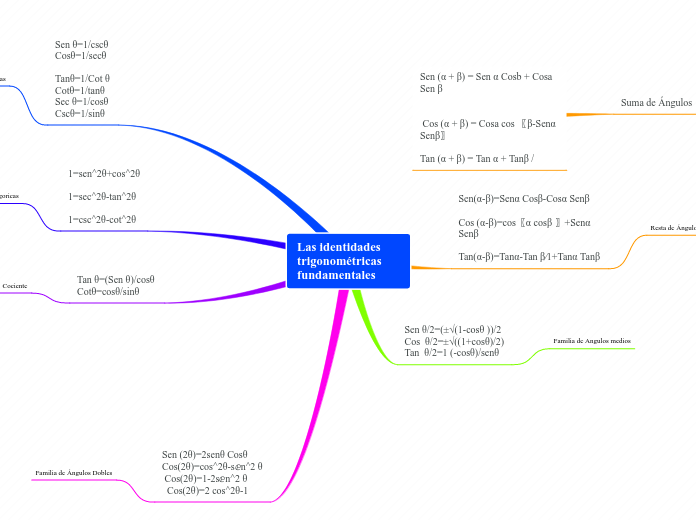
trigonometria
Las identidades trigonométricas son herramientas fundamentales en matemáticas, proporcionando relaciones esenciales entre las funciones seno, coseno y tangente, entre otras. Estas identidades permiten simplificar y resolver problemas complejos relacionados con ángulos y sus sumas, diferencias y duplicaciones.