Trigonometry
Trigonometric Equations
Steps to solve
Write solutions
Always write as ordered pairs when is more than one solution)
x=(0,2π)
Use the General Formula
k is any integer
One should know their angles and how to identify
when to stop due to restrictions.
Helps you find the solutions as requested
θ+2kπ
0+2kπ
Find the angle
cosθ=1
θ=0
Identify the equation
cosθ=1, when ,0≤ θ ≤2π
Observe the restrictions
See what function is being used
Solutions to equations are values of the variable
that make the equation a true statement.
It is used to find all x solutions
Solving equations is a technique that has been used since early Algebra courses.
Trigonometric Functions
Reciprocal Functions
Cotangent Function
x=coty
y=cot^(-1)x
arccot
cot^(-1) θ
Properties
x/y
any θ
cotθ=x/y
Since radius is not needed to find cotangent,
the equation is the same in all kinds of circles
cot
cos/sin
1/tan
Secant Function
0≤y≤π, y≠ π/2
x=secy
y=sec^(-1)x
arcsec
sec^(-1) θ
1/x
input
any θ
cscθ=r/x
Since radius is more than one, the result is r divided by x
cscθ=1/x
Since in a unit circle radius is one, the result is one over x
sec
1/cos
Cosecant Funtion
-π/2≤y≤π/2, y≠0
|x|≥1
x=cscy
y=csc^(-1)x
arccsc
csc^(-1) θ
all real numbers greater than or equal to 1 or less than or equal to -1
All real numbers except integer multiples of π
1/y
Any θ that does not produce division by zero
2√3/3
√2
2
Value Within Points
y≠0
cscθ=r/y
Since radius is more than one, radius should be divided by y
In a unit circle
cscθ=1/y
Since in a unit circle the radius is one, the result is one over y
cscθ
1/sinθ
Primary Functions
Tangent function
-π/2
x=tany
y=tan^(-1)x
arctan
tan^(-1) θ
All real numbers
All real numbers except odd integeres multiples of π/2
y/x
any θ that does not produce division by zero
Measurement
Undefined
√3
pi/4
√3/3
Associates with the ratio of the y-coordinate
to the x-coordinate)
Value within points
x≠0
tanθ=x/y
Since radius is not neded to find tangent,
the equation is the same in all kind of circles
tanθ
sinθ/cosθ
cosine function
[0,π]
x=cosy
y=cos^(-1)x
arccos
cos^(-1) θ
x
In Different Circles
cosθ=x/r
Since the radius is more than one, x should
be divided by r
cosθ=x/1
Since in a unit circle the radius, or hypotenuse, is one, the result is x
Associates each angle with the horizontal
coordinate (x-coordinate)
cos
sine function
Inverse
[-π/2,π/2]
x=siny
y=sin^(-1)x
arcsin
sin^(-1) θ
Properties
Range
[-1,1]
Domain
All Real Numbers
Output
y
Input
Measurements
360
2π
-1
270
3π/2
180
π
1
90
π/2
√3/2
60
π/3
√2/2
45
π/4
1/2
30
π/6
0
Value within Points
In a Different Circles
sinαθ=y/r
Since the radius is more than one, y should
be divided by r
In a Unit Circle
sinθ= y/1
Since in a unit circle the radius, or hypotenuse, is one, the result is y
Asoociates each angle with the vertical
coordinate (y-coordinate)
sin
Uses Greek letter to denote angles
Theta
θ
Gamma
γ
Beta
β
Alpha
α
Important in Modeling of periodic Phenomena.
Used to relate the angles of a triangle
to the lengths of the sides of a triangle
Circular Functions
Functions of an Angle
Equations
Transformations
Trig
Horizontal Shift: ϕ/ω
Period: T=2π/ω
A is amplitude, ω is omega, φ is phi
f ( x )= A sin ( ωx−φ ) + B= A sin (ω (x− φ/ω ) )+ B
Normal
a is the vertical stretch/compression
b is the Horizontal stretch/compression
h is the horizontal shift and k is the vertical shift
g(x)=af(b(x-h))+k
Odd Properties
f(-θ)=-f(θ)
Even Properties
f(-θ)=θ
Period of Trig Functions
Tangent/Cotangent
Their Period is π
θ+πk=θ
Sine/Cosine/Cosecant/Secant
Their Period is 2π
θ+2πk=θ
Radius
Subtopic
For an angle in standard position, let P=(x,y) be the point on the
terminal side of the angle that is also on the circle .
x^2+y^2=r^2
Periodic Point
This is used to find points through the unit circle
P=(cosθ, sinθ)
P=(x, y)
Area of a Sector of a circle
The area of a sector of a circle is
proportional to the measure of the central angle.
This can only be done in radians
A=1/2 r^2 θ
Revolution of a unit circle
This is used to find the outside measure of a unit circle
C=360
C=2π
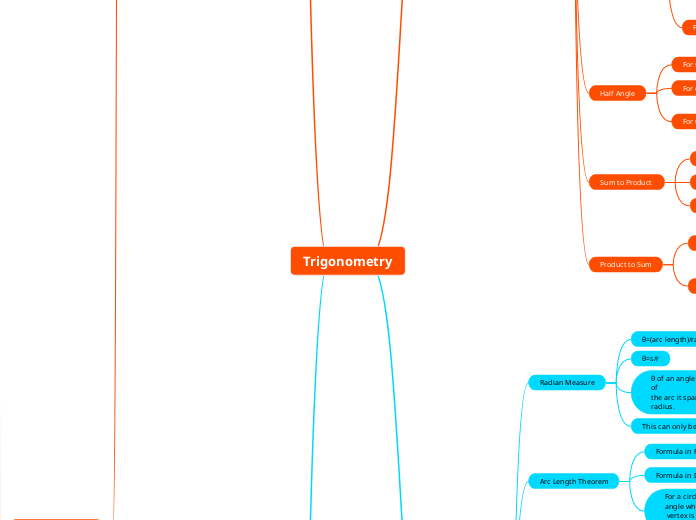
Arc Length Theorem
For a circle of radius r, a central angle (a positive angle whose
vertex is at the center of a circle) of θ radians subtends an arc whose length is s
Formula in Degrees
s=(θ/360)2πr
Formula in Radians
s=θr
Radian Measure
This can only be done in Radians
θ of an angle is the measure of the ratio of length of
the arc it spans on the circle to the length of the radius.
θ=s/r
θ=(arc length)/radius
Trigonometric Identities
Product to Sum
cosα-cosβ=-2(sin (α+β)/2) (sin (α-β)/2)
cosα+cosβ=2(cos (α+β)/2) (cos (α-β)/2)
sinα-sinβ=2(sin (α-β)/2) (cos (α+β)/2)
sinα+sinβ=2(sin (α+β)/2) (cos (α-β)/2)
Sum to Product
For sine and cosine
sinα cosβ=1/2[sin(α+β)-sin(α-β)]
cosα cosβ=1/2[cos(α-β)+cos(α+β)]
For sine
sinα sinβ=1/2[cos(α-β)-cos(α+β)]
Half Angle
tan ∝/2=(1-cos∝)/(sin∝)
tan ∝/2=±√((1-cos∝)/(1+cos∝))
cos ∝/2=±√((1+cos∝)/2)
sin ∝/2=±√((1-cos∝)/2)
Double Angle
tan^2 θ=(1-cos(2θ))/(1+cos(2θ))
tan(2θ)=2tanθ/(1-tanθ)
cos^2 θ=(1+cos(2θ))/2
cos(2θ)=2cos^2 θ-1
cos(2θ)=1-2sin^2 θ
cos(2θ)=cos^2 θ+sin^2 θ
sin^2 θ=1-cos(2θ)/2
sin(2θ)=2sinθcosθ
Sum/Difference
For tangent
tan(α-β)=(tanα - tanβ)/(1+(tanα tanβ) )
tan(α+β)=(tanα + tanβ)/(1-(tanα tanβ) )
For sine
sin(a-b)=sina cosb-cosa sinb
sin(a+b)=sina cosb+cosa sinb
For cosine
cos(a-b)=cosa cosb+sina sinb
cos(a+b)=cosa cosb-sina sinb
Even
Evens with a negative angle results as positive
sec(-θ)=secθ
cos(-θ)=cosθ
Odd
Odds with a negative angle results as negative
cot(-θ)=-cotθ
tan(-θ)=-tanθ
csc(-θ)=-cscθ
sin(-θ)=-sinθ
Pythagorean
Each Pythagorean Identity is connected since each uses the prymary identity but some uses reciprocal too
cscθ^2-cotθ^2=1
secθ^2-tanθ^2=1
sinθ^2+cosθ^2=1
Reciprocal
Each primary function has a reciprocal identity
cotθ=1/tanθ
secθ=1/cosθ
cscθ=1/sinθ
Quotient
Just tanθ and cotθ are the only functions that hace Quotient Idebtities
cotθ=cosθ/sinθ
tanθ=sinθ/cosθ